
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác abc ( a=90 độ). giải tam giác vuông abc biết a)AB =30cm , acb=30 độ b) AB=20cm ;AC=13cm

a.
Trong tam giác vuông ABC:
\(tan\widehat{ACB}=\dfrac{AB}{AC}\Rightarrow AC=AB.tan\widehat{ACB}=30.tan30^0=10\sqrt{3}\left(cm\right)\)
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=20\sqrt{3}\left(cm\right)\)
\(\widehat{ABC}=90^0-\widehat{ACB}=60^0\)
b.
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{569}\left(cm\right)\)
\(tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{13}{20}\Rightarrow\widehat{ABC}\approx33^0\)
\(\widehat{ACB}=90^0-\widehat{ABC}=57^0\)

a.
$\widehat{C}=90^0-\widehat{B}=90^0-58^0=32^0$
$\cos B=\frac{c}{a}\Rightarrow c=a\cos B=72\cos 58^0=38,15$ (cm)
$\sin B=\frac{b}{a}\Rightarrow b=a\sin B=72\sin 58^0=61,06$ (cm)
b.
$\widehat{C}=90^0-\widehat{B}=90^0-40^0=50^0$
$\sin B=\frac{b}{a}\Rightarrow a=\frac{b}{\sin B}=\frac{20}{\sin 40^0}=31,11^0$
$\tan B=\frac{b}{c}\Rightarrow c=\frac{20}{\tan 40^0}=23,84^0$
c.
$\widehat{B}=90^0-\widehat{C}=90^0-30^0=60^0$
$\tan B=\frac{b}{c}\Rightarrow c=\frac{b}{\tan B}=\frac{15}{\tan 60^0}=5\sqrt{3}$ (cm)
$\sin B=\frac{b}{a}\Rightarrow a=\frac{b}{\sin B}=\frac{15}{\sin 60^0}=10\sqrt{3}$ (cm)
d
$a=\sqrt{b^2+c^2}=\sqrt{21^2+18^2}=3\sqrt{85}$ (cm)
$\tan B=\frac{b}{c}=\frac{21}{18}=\frac{7}{6}$
$\Rightarrow \widehat{B}=49,4^0$
$\widehat{C}=90^0-\widehat{B}=40,6^0$

Lời giải:
$S_{ABC}=AH.BC:2=12.20:2=120$ (cm2)
Thông tin A=90 độ không có ý nghĩa gì trong bài.


Trong tam giác vuông ABC:
\(cosB=\dfrac{AB}{BC}\Rightarrow AB=BC.cosB\)
Trong tam giác vuông ABH:
\(sinB=\dfrac{AH}{AB}\Rightarrow AH=AB.sinB=BC.sinB.cosB=6.sin55^0.cos55^0\approx2,8\left(cm\right)\)
\(cosB=\dfrac{BH}{AB}\Rightarrow BH=AB.cosB=BC.\left(cosB\right)^2=6.\left(cos55^0\right)^2\approx1,2\left(cm\right)\)
\(CH=BC-BH=6-1,2=4,8\left(cm\right)\)

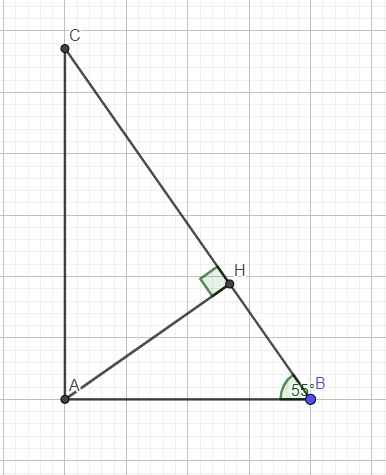
góc C = 90-55=35 độ
a=20cm=BC
=>AC=sin(55).BC=sin(55).20=16.383 cm ( tam giác ABC vuông áp dụng lượng giác)
=> AB=cos (55). BC=cos(55).20=11.471 cm (tam giác ABC vuông áp dụng hệ thức lượng)