
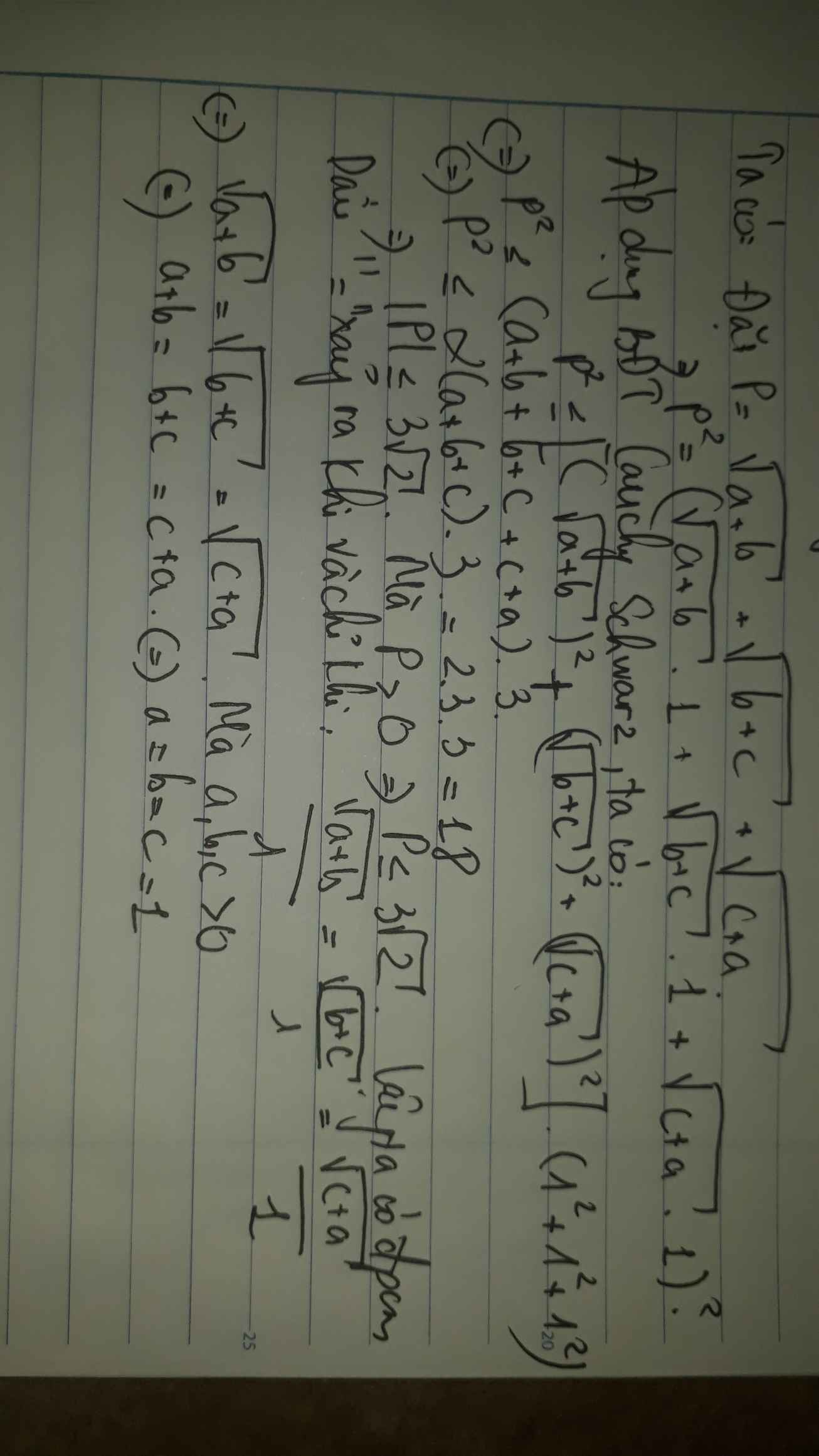
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

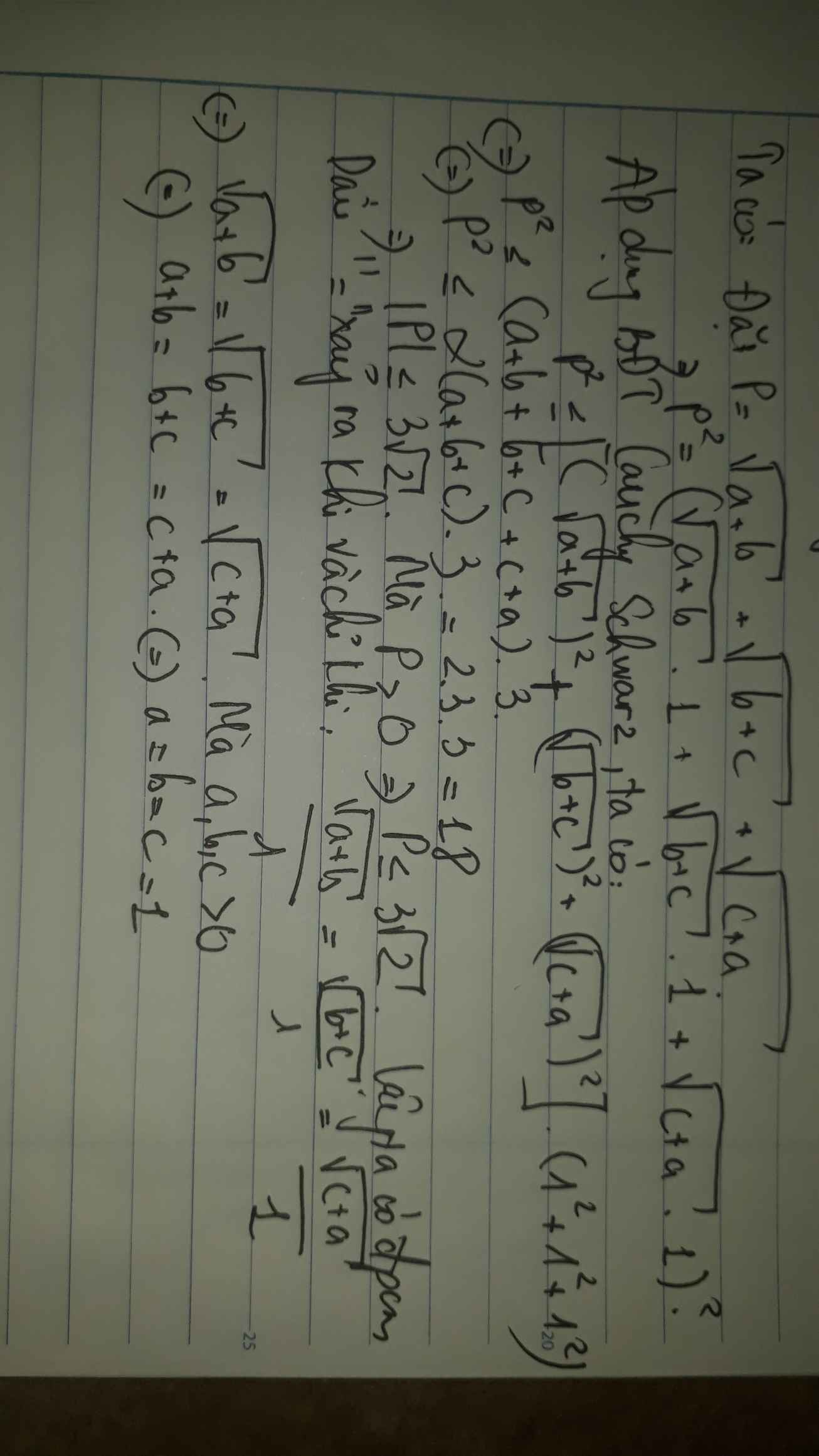

1) \(\Sigma\frac{a}{b^3+ab}=\Sigma\left(\frac{1}{b}-\frac{b}{a+b^2}\right)\ge\Sigma\frac{1}{a}-\Sigma\frac{1}{2\sqrt{a}}=\Sigma\left(\frac{1}{a}-\frac{2}{\sqrt{a}}+1\right)+\Sigma\frac{3}{2\sqrt{a}}-3\)
\(\ge\Sigma\left(\frac{1}{\sqrt{a}}-1\right)^2+\frac{27}{2\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)}-3\ge\frac{27}{2\sqrt{3\left(a+b+c\right)}}-3=\frac{3}{2}\)

Đề đúng là: Cho \(a,b,c>0\) thỏa mãn \(\sqrt{a}+\sqrt{b}-\sqrt{c}=\sqrt{a+b-c}\)
Chứng minh \(\sqrt[2006]{a}+\sqrt[2006]{b}-\sqrt[2006]{c}=\sqrt[2006]{a+b-c}\)
Giải: Từ \(\sqrt{a}+\sqrt{b}-\sqrt{c}=\sqrt{a+b-c}\)\(\Rightarrow\)\(\left(\sqrt{a}+\sqrt{b}-\sqrt{c}\right)^2=\left(\sqrt{a+b-c}\right)^2\)
\(\Leftrightarrow\)\(a+b+c+2\sqrt{ab}-2\sqrt{bc}-2\sqrt{ca}=a+b-c\)
\(\Leftrightarrow\)\(2c+2\sqrt{ab}-2\sqrt{bc}-2\sqrt{ca}=0\)
\(\Leftrightarrow\)\(\left(c-\sqrt{ca}\right)+\left(\sqrt{ab}-\sqrt{bc}\right)=0\)
\(\Leftrightarrow\)\(\sqrt{c}\left(\sqrt{c}-\sqrt{a}\right)-\sqrt{b}\left(\sqrt{c}-\sqrt{a}\right)=0\)
\(\Leftrightarrow\)\(\left(\sqrt{c}-\sqrt{a}\right)\left(\sqrt{c}-\sqrt{b}\right)=0\)
\(\Rightarrow\)\(\sqrt{c}-\sqrt{a}=0\) hoặc \(\sqrt{c}-\sqrt{b}=0\)\(\Rightarrow\)\(\sqrt{c}=\sqrt{a}\) hoặc \(\sqrt{c}=\sqrt{b}\)
- Nếu \(\sqrt{c}=\sqrt{a}\) thì \(\sqrt[2006]{a}+\sqrt[2006]{b}-\sqrt[2006]{c}=\sqrt[2006]{b}=\sqrt[2006]{a+b-c}\)
- Nếu \(\sqrt{c}=\sqrt{b}\) thì \(\sqrt[2006]{a}+\sqrt[2006]{b}-\sqrt[2006]{c}=\sqrt[2006]{a}=\sqrt[2006]{a+b-c}\)
chịu .chưa học ai cũng chưa học giống mình thì k cho mình .rồi mình k lại cho.thề đấy

3, \(\sqrt{\frac{a}{b+c}}=\sqrt{\frac{a^2}{a\left(b+c\right)}}\Rightarrow\frac{1}{\sqrt{\frac{a}{b+c}}}=\sqrt{\frac{a\left(b+c\right)}{a^2}}.\)
Áp dụng bất đẳng thức Cô si ta có : \(\sqrt{\frac{a\left(b+c\right)}{a^2}}\le\frac{a+b+c}{2a}\Rightarrow\sqrt{\frac{a}{b+c}}\ge\frac{2a}{a+b+c}\left(1\right).\)
Chứng minh tương tự ta có : \(\sqrt{\frac{b}{a+c}}\ge\frac{2b}{a+b+c}\left(2\right).\); \(\sqrt{\frac{c}{a+b}}\ge\frac{2c}{a+b+c}\left(3\right).\)
Cộng vế với vế các bất đẳng thức cùng chiều ta được:
\(\sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{a+c}}+\sqrt{\frac{c}{a+b}}\ge\frac{2\left(a+b+c\right)}{a+b+c}=2.\)( đpcm )
dấu " = " xẩy ra khi a = b = c > 0

\(VT\le\frac{1}{\sqrt[3]{9}}\left(\frac{a+2b+3+3}{3}+\frac{b+2c+3+3}{3}+\frac{c+2a+3+3}{3}\right)\)
\(=\frac{1}{\sqrt[3]{9}}.\frac{3\left(a+b+c\right)+18}{3}=\frac{9}{\sqrt[3]{9}}=\sqrt[3]{81}=3\sqrt[3]{3}\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(a=b=c=1\)

gt <=> \(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}=1\)
Đặt: \(\frac{1}{a}=x;\frac{1}{b}=y;\frac{1}{c}=z\)
=> Thay vào thì \(VT=\frac{\frac{1}{xy}}{\frac{1}{z}\left(1+\frac{1}{xy}\right)}+\frac{1}{\frac{yz}{\frac{1}{x}\left(1+\frac{1}{yz}\right)}}+\frac{1}{\frac{zx}{\frac{1}{y}\left(1+\frac{1}{zx}\right)}}\)
\(VT=\frac{z}{xy+1}+\frac{x}{yz+1}+\frac{y}{zx+1}=\frac{x^2}{xyz+x}+\frac{y^2}{xyz+y}+\frac{z^2}{xyz+z}\ge\frac{\left(x+y+z\right)^2}{x+y+z+3xyz}\)
Có BĐT x, y, z > 0 thì \(\left(x+y+z\right)\left(xy+yz+zx\right)\ge9xyz\)Ta thay \(xy+yz+zx=1\)vào
=> \(x+y+z\ge9xyz=>\frac{x+y+z}{3}\ge3xyz\)
=> Từ đây thì \(VT\ge\frac{\left(x+y+z\right)^2}{x+y+z+\frac{x+y+z}{3}}=\frac{3}{4}\left(x+y+z\right)\ge\frac{3}{4}.\sqrt{3\left(xy+yz+zx\right)}=\frac{3}{4}.\sqrt{3}=\frac{3\sqrt{3}}{4}\)
=> Ta có ĐPCM . "=" xảy ra <=> x=y=z <=> \(a=b=c=\sqrt{3}\)

Ta có:
\(a^3+1+1+b^3+1+1+c^3+1+1\ge3\left(a+b+c\right)\)
\(\Rightarrow3\left(a+b+c\right)\le a^3+b^3+c^3+6\le9\)
\(\Rightarrow a+b+c\le3\)
\(\Rightarrow ab+bc+ca\le\frac{\left(a+b+c\right)^2}{3}\le3\)
Quay lại bài toán ta có:
\(\left(\frac{ab}{\sqrt{c+3}}+\frac{bc}{\sqrt{a+3}}+\frac{ca}{\sqrt{b+3}}\right)^2\le\left(ab+bc+ca\right)\left(\frac{ab}{c+3}+\frac{bc}{a+3}+\frac{ca}{b+3}\right)\)
\(\le3.\left(\frac{ab}{c+3}+\frac{bc}{a+3}+\frac{ca}{b+3}\right)\)
\(\le3.\left(\frac{ab}{c+a+c+b}+\frac{bc}{a+b+a+c}+\frac{ca}{b+a+b+c}\right)\)
\(\le\frac{3}{4}.\left(\frac{ab}{c+a}+\frac{ab}{b+c}+\frac{bc}{a+b}+\frac{bc}{c+a}+\frac{ca}{a+b}+\frac{ca}{b+c}\right)\)
\(=\frac{3}{4}.\left(\frac{ca}{a+b}+\frac{bc}{a+b}+\frac{bc}{c+a}+\frac{ab}{c+a}+\frac{ca}{b+c}+\frac{ab}{b+c}\right)\)
\(=\frac{3}{4}.\left(a+b+c\right)\le\frac{9}{4}\)
\(\Rightarrow\frac{ab}{\sqrt{c+3}}+\frac{bc}{\sqrt{a+3}}+\frac{ca}{\sqrt{b+3}}\le\frac{3}{2}\)
\(\Rightarrow\frac{2ab}{\sqrt{c+3}}+\frac{2bc}{\sqrt{a+3}}+\frac{2ca}{\sqrt{b+3}}\le3\)
PS: Được chưa 2 cô nương Hoàng Lê Bảo Ngọc, Witch Rose.
Số t khổ quá mà. Thấy có bài giải mừng húm tưởng khỏi cần giải nữa thì vô đọc bài của bác Thắng Nguyễn thấy mệt mệt. Bác lo mà úp mặt vô tường đi :(
Cái này xấu lắm đấy nhé :v, chủ thớt muốn thì post thôi @@
*)Note:\(Σ\) là tổng đối xứng viết tắt cho gọn
\(\text{∏}\) tích đối xứng viết tắt luôn :v \(\text{∏}a=abc;Σa=a+b+c\)
\(BDT\Leftrightarrow\frac{ab}{\sqrt{c+3}}+\frac{bc}{\sqrt{a+3}}+\frac{ca}{\sqrt{b+3}}\le\frac{3}{2}\)
Theo Cauchy-Schwarz và đặt \(a+b+c=3u;ab+bc+ca=3v^2;abc=w^3\)
\(\left(Σ\frac{ab}{\sqrt{c+3}}\right)^2\leΣab\cdotΣ\frac{ab}{c+3}\le\frac{9}{4}\)
\(\Leftrightarrow\frac{3v^2Σab\left(a+3\right)\left(b+c\right)}{\text{∏}\left(a+3\right)}\le\frac{9}{4}\)
\(\Leftrightarrow4v^2Σ\left(a^2b^2+3a^2b+3a^2c+9ab\right)\le3\left(abc+27+Σ\left(3ab+9a\right)\right)\)
\(\Leftrightarrow4v^2\left(9v^4-6uw^3+27uv^2-9w^3+27v^2\right)\le3\left(w^3+9v^2+27+27u\right)\)
\(\Leftrightarrow w^3\left(1+12v^2+8uv^2\right)+27u+27+9v^2\ge12v^6+36uv^4+36v^4\)
A[ dụng BDT Schur có:\(w^3\ge4uv^2-3u^3\)
Nên cần cm \(\left(4uv^2-3u^3\right)\left(1+12v^2+8uv^2\right)+27u+27+9v^2\ge12v^6+36uv^4+36v^4\)
\(\Leftrightarrow32u^2v^4+12uv^4+4uv^2+9v^2+27u+27\ge12v^6+36v^4+3u^3+24u^2v^2+36u^3v^2\)
Đúng theo BĐT P-M và BĐT AM-GM
P.s: Đọc đến đây thì cho hỏi cái đề đâu ra thế, thật sự lm ko muốn dùng cách này đâu @@ hại não, hại mắt