
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)

Mình khuyên bạn thế này :
Bạn nên tách những câu hỏi ra
Như vậy các bạn sẽ dễ giúp
Và cũng có nhiều bạn giúp hơn !
Bài 1.
a) ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
Vậy S = { 3 ; -7 }
b) ( x - 2 )2 + ( x - 2 )( x - 3 ) = 0
<=> ( x - 2 )( x - 2 + x - 3 ) = 0
<=> ( x - 2 )( 2x - 5 ) = 0
<=> x - 2 = 0 hoặc 2x - 5 = 0
<=> x = 2 hoặc x = 5/2
Vậy S = { 2 ; 5/2 }
c) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> x - 2 = 0 hoặc x - 3 = 0
<=> x = 2 hoặc x = 3

(x^2+x)^2+4(x^2+x)=12
<=>x^4 + 2x^3 + x^2 + 4x^2 + 4x - 12 = 0
<=>x^4 + 2x^3 + 5x^2 + 10x - 6x - 12 = 0
<=>x^3(x+2) + 5x(x+2)-6(x+2) = 0
<=>(x+2)(x^3 + 5x - 6) = 0
<=>(x+2)(x^3 - x+ 6x - 6) =0
<=>(x+2)[(x-1)(x^2+x+1) + 6(x-1)] = 0
<=>(x+2)(x-1)(x^2+x+7) = 0
Ta có: x^2+x+7 >=0
<=>
[ x+2 = 0 <=> x = -2
[x - 1 = 0 <=> x = 1
Vậy pt có 2 ng x=1, x=-2
Đặt ẩn phụ là xong á?
Đặt \(x^2+x=t\).Phương trình trở thành:
\(t^2+4t-12=0\Leftrightarrow t^2-2t+6t-12=0\)
\(\Leftrightarrow t\left(t-2\right)+6\left(t-2\right)=0\)
\(\Leftrightarrow\left(t-2\right)\left(t+6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t=2\\t=-6\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2+x-2=0\left(1\right)\\x^2+x+6=0\left(2\right)\end{cases}}\)
Giải (1) được hai nghiệm: x = 1; x = -2
Giải (2) ta có: \(x^2+x+6=\left(x+\frac{1}{2}\right)^2+\frac{23}{4}>0\forall x\)
Nên (2) vô nghiệm.
Vậy phương trình có 2 nghiệm x = 1; x = -2

a) \(2x-10=0\)
\(\Leftrightarrow2x=10\)
\(\Leftrightarrow x=5\)
Vậy tập nghiệm của phương trình là: S = {5}
b) \(3,4-x=-4\)
\(\Leftrightarrow x=7,4\)
Vậy tập nghiệm của phương trình là: S = {7,4}
c) \(x-\frac{4}{5}=\frac{1}{5}\)
\(\Leftrightarrow x=1\)
Vậy tập nghiệm của phương trình là: S = {1}
d) \(2\left(x-3\right)-3x+5=0\)
\(\Leftrightarrow2x-6-3x+5=0\)
\(\Leftrightarrow-x-1=0\)
\(\Leftrightarrow x=-1\)
Vậy tập nghiệm của phương trình là: S = {-1}
a, \(2x-10=0\Leftrightarrow x=5\)
Vậy tập nghiệm của phương trình là S = {5}
b, \(3,4-x=-4\Leftrightarrow x=7,4\)kết luận tương tự như trên và các phần còn lại
c, \(\frac{x-4}{5}=\frac{1}{5}\)Khử mẫu : \(x-4=1\Leftrightarrow x=5\)
d, \(x+12=2-x\Leftrightarrow2x=-10\Leftrightarrow x=-5\)
e, \(2\left(x-3\right)-3x+5=0\Leftrightarrow2x-6-3x+5=0\)
\(\Leftrightarrow-x-1=0\Leftrightarrow x=-1\)


`a,(2x-5)(12+5x)=0`
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\12+5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\5x=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{12}{5}\end{matrix}\right.\)
`b, (x-3)(x-4)-2(x-3)=0`
`<=>(x-3)(x-4-2)=0`
`<=>(x-3)(x-6)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=6\end{matrix}\right.\)
`c, x(x-1)(x+1)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
`d, (2x)/3 +(2x-1)/6=0`
`<=> (4x)/6 +(2x-1)/6=0`
`<=> (4x+2x-1)/6=0`
`<=> (6x-1)/6=0`
`<=> 6x-1=0`
`<=> 6x=1`
`<=>x=1/6` ( đề là vậy à bạn )
a) \(\left(2x-5\right)\left(12+5x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\12+5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\5x=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2,5\\x=-2,4\end{matrix}\right.\)
b) \(\left(x-3\right)\left(x-4\right)-2\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left[\left(x-4\right)-2\right]=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-6\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=6\end{matrix}\right.\)
c) \(x\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\\x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\\x=0\end{matrix}\right.\)
d) \(\dfrac{2x}{3}+\dfrac{2x-1}{6}=0\)
\(\Leftrightarrow\dfrac{4x+2x-1}{6}=0\)
\(\Leftrightarrow6x-1=0\)
\(\Leftrightarrow6x=1\Leftrightarrow x=\dfrac{1}{6}\)


1. Ta có \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16=0\)
\(\Rightarrow\)\(\left[\left(x+2\right)\left(x+8\right)\right].\left[\left(x+4\right)\left(x+6\right)\right]+16=0\)
\(\Rightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16=0\)
Đặt \(x^2+10x=t\)
Pt \(\Leftrightarrow\left(t+16\right)\left(t+24\right)+16=0\Leftrightarrow t^2+40t+400=0\Leftrightarrow t=-20\)
\(\Rightarrow x^2+10x+20=0\Rightarrow\orbr{\begin{cases}x=-5+\sqrt{5}\\x=-5-\sqrt{5}\end{cases}}\)
2. Ta có \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24=0\)
\(\Rightarrow\left[\left(x+2\right)\left(x+5\right)\right].\left[\left(x+3\right)\left(x+4\right)\right]-24=0\)\(\Rightarrow\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24=0\)
Đặt \(x^2+7x=t\Rightarrow\left(t+10\right)\left(t+12\right)-24=0\Rightarrow t^2+22t+96=0\)\(\Rightarrow\orbr{\begin{cases}t=-6\\t=-16\end{cases}}\)
Với \(t=-6\Rightarrow x^2+7x+6=0\Rightarrow\orbr{\begin{cases}x=-6\\x=-1\end{cases}}\)
Với \(t=-16\Rightarrow x^2+7x+16=0\left(l\right)\)
Vậy pt có 2 nghiệm là \(\orbr{\begin{cases}x=-6\\x=-1\end{cases}}\)
Quản lí Hoàng Thị Lan Hương giúp em giải bài toán vừa đăng lên đc ko ạ.??? ^^
⇔ ( x + 2 )( x - 1 ) = 0 ⇔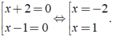
Vậy phương trình có tập nghiệm là S = { - 2;1 }.