PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 1 2021
Câu 1 :
a, \(\frac{3\left(2x+1\right)}{4}-\frac{5x+3}{6}=\frac{2x-1}{3}-\frac{3-x}{4}\)
\(\Leftrightarrow\frac{6x+3}{4}+\frac{3-x}{4}=\frac{2x-1}{3}+\frac{5x+3}{6}\)
\(\Leftrightarrow\frac{5x+6}{4}=\frac{9x+1}{6}\Leftrightarrow\frac{30x+36}{24}=\frac{36x+4}{24}\)
Khử mẫu : \(30x+36=36x+4\Leftrightarrow-6x=-32\Leftrightarrow x=\frac{32}{6}=\frac{16}{3}\)
tương tự
PN
16 tháng 5 2021
\(\frac{19}{4}-\frac{2\left(3x-5\right)}{5}=\frac{3-2x}{10}-\frac{3x-1}{4}\)
\(< =>\frac{19.5}{20}-\frac{8\left(3x-5\right)}{20}=\frac{2\left(3-2x\right)}{20}-\frac{5\left(3x-1\right)}{20}\)
\(< =>95-24x+40=6-4x-15x+5\)
\(< =>-24x+135=-19x+11\)
\(< =>5x=135-11=124\)
\(< =>x=\frac{124}{5}\)
26 tháng 5 2021
1) \(3x-2x+6=6\Leftrightarrow x=0\)
2) \(4\left(2x-1\right)-12x-12=3\left(x+2\right)\)
\(\Leftrightarrow8x-4-12x-12-3x-6=0\)
\(\Leftrightarrow7x=-22\Leftrightarrow x=\dfrac{-22}{7}\)
TB
26 tháng 5 2021
3, \(\left(x-1\right)2=9\left(x+1\right)2\)
\(\Leftrightarrow2x-2\) \(=18x+18\)
\(\Leftrightarrow2x-18x=18+2\)
\(\Leftrightarrow-16x\) \(=20\)
\(\Leftrightarrow x\) \(=\dfrac{-5}{4}\)
Vậy pt đã cho có tập nghiệm là S= \(\left\{\dfrac{-5}{4}\right\}\)
4, \(\dfrac{x-4}{x-1}+\dfrac{x+4}{x+1}=2\) ( ĐKXĐ : \(x\ne\pm1\) )
\(\Leftrightarrow\dfrac{\left(x-4\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{\left(x+4\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{2\left(x+1\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow x^2-3x-4+x^2+3x-4=2x^2-2\)
\(\Leftrightarrow2x^2-8-2x^2+2=0\)
\(\Leftrightarrow0\) \(=6\) ( Vô lí )
Vậy pt đã cho vô nghiệm
9 tháng 2 2022
a: \(\Leftrightarrow\left(4x+14\right)^2-\left(3x+9\right)^2=0\)
=>(4x+14+3x+9)(4x+14-3x-9)=0
=>(7x+23)(x+5)=0
=>x=-23/7 hoặc x=-5
9 tháng 2 2022
\(a,\\ \Leftrightarrow7x^2+58x+115=0\\ \Leftrightarrow\left(x+5\right)\left(7x+23\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x+5=0\\7x+23=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-5\\x=-\dfrac{23}{7}\end{matrix}\right.\)
\(b,\\ \Leftrightarrow\left[\left(x+1\right)\left(x+5\right)\right]\left[\left(x+3\right)\left(x+4\right)\right]=0\\ \Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+8\right)=0\\ \LeftrightarrowĐặt.x^2+6x+5=a\\ \Leftrightarrow a=a\left(a+3\right)=10\\ \Leftrightarrow a^2+3a-10=0\\ \Leftrightarrow\left(a+5\right)\left(a-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=-5\\a=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x^2+6x+5=-5\\x^2+6x+5=2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x^2+6x+10=0\\x^2+6x+3=0\end{matrix}\right.\\ \left(Vô.n_o\Delta=36-40=-4< 0\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3+\sqrt{6}\\x=-3-\sqrt{6}\end{matrix}\right.\)
VD
18 tháng 3 2022
\(a,4+3x=25-4x\\ \Leftrightarrow7x=21\\ \Leftrightarrow x=3\\ b,\left(x-1\right)^2+\left(x-1\right)\left(x+3\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-1+x+3\right)=0\\ \Leftrightarrow\left(x-1\right)\left(2x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
c, ĐKXĐ:\(x\ne-1,x\ne2\)
\(\dfrac{1}{x+1}+\dfrac{3}{x-2}=\dfrac{9}{\left(x+1\right)\left(x-2\right)}\\ \Leftrightarrow\dfrac{x-2}{\left(x+1\right)\left(x-2\right)}+\dfrac{3\left(x+1\right)}{\left(x+1\right)\left(x-2\right)}-\dfrac{9}{\left(x+1\right)\left(x-2\right)}=0\\ \Leftrightarrow\dfrac{x-2+3x+3-9}{\left(x+1\right)\left(x-2\right)}=0\\ \Rightarrow4x-8=0\\ \Leftrightarrow x=2\left(ktm\right)\)
S
23 tháng 2 2021
Mình khuyên bạn thế này :
Bạn nên tách những câu hỏi ra
Như vậy các bạn sẽ dễ giúp
Và cũng có nhiều bạn giúp hơn !
23 tháng 2 2021
Bài 1.
a) ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
Vậy S = { 3 ; -7 }
b) ( x - 2 )2 + ( x - 2 )( x - 3 ) = 0
<=> ( x - 2 )( x - 2 + x - 3 ) = 0
<=> ( x - 2 )( 2x - 5 ) = 0
<=> x - 2 = 0 hoặc 2x - 5 = 0
<=> x = 2 hoặc x = 5/2
Vậy S = { 2 ; 5/2 }
c) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> x - 2 = 0 hoặc x - 3 = 0
<=> x = 2 hoặc x = 3
25 tháng 4 2020
Bài 1:
a) (5x-4)(4x+6)=0
\(\Leftrightarrow\orbr{\begin{cases}5x-4=0\\4x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}5x=4\\4x=-6\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{4}{5}\\y=\frac{-3}{2}\end{cases}}}\)
b) (x-5)(3-2x)(3x+4)=0
<=> x-5=0 hoặc 3-2x=0 hoặc 3x+4=0
<=> x=5 hoặc x=\(\frac{3}{2}\)hoặc x=\(\frac{-4}{3}\)
c) (2x+1)(x2+2)=0
=> 2x+1=0 (vì x2+2>0)
=> x=\(\frac{-1}{2}\)
30 tháng 4 2020
bài 1:
a) (5x - 4)(4x + 6) = 0
<=> 5x - 4 = 0 hoặc 4x + 6 = 0
<=> 5x = 0 + 4 hoặc 4x = 0 - 6
<=> 5x = 4 hoặc 4x = -6
<=> x = 4/5 hoặc x = -6/4 = -3/2
b) (x - 5)(3 - 2x)(3x + 4) = 0
<=> x - 5 = 0 hoặc 3 - 2x = 0 hoặc 3x + 4 = 0
<=> x = 0 + 5 hoặc -2x = 0 - 3 hoặc 3x = 0 - 4
<=> x = 5 hoặc -2x = -3 hoặc 3x = -4
<=> x = 5 hoặc x = 3/2 hoặc x = 4/3
c) (2x + 1)(x^2 + 2) = 0
vì x^2 + 2 > 0 nên:
<=> 2x + 1 = 0
<=> 2x = 0 - 1
<=> 2x = -1
<=> x = -1/2
bài 2:
a) (2x + 7)^2 = 9(x + 2)^2
<=> 4x^2 + 28x + 49 = 9x^2 + 36x + 36
<=> 4x^2 + 28x + 49 - 9x^2 - 36x - 36 = 0
<=> -5x^2 - 8x + 13 = 0
<=> (-5x - 13)(x - 1) = 0
<=> 5x + 13 = 0 hoặc x - 1 = 0
<=> 5x = 0 - 13 hoặc x = 0 + 1
<=> 5x = -13 hoặc x = 1
<=> x = -13/5 hoặc x = 1
b) (x^2 - 1)(x + 2)(x - 3) = (x - 1)(x^2 - 4)(x + 5)
<=> x^4 - x^3 - 7x^2 + x + 6 = x^4 + 4x^3 - 9x^2 - 16x + 20
<=> x^4 - x^3 - 7x^2 + x + 6 - x^4 - 4x^3 + 9x^2 + 16x - 20 = 0
<=> -5x^3 - 2x^2 + 17x - 14 = 0
<=> (-x + 1)(x + 2)(5x - 7) = 0
<=> x - 1 = 0 hoặc x + 2 = 0 hoặc 5x - 7 = 0
<=> x = 0 + 1 hoặc x = 0 - 2 hoặc 5x = 0 + 7
<=> x = 1 hoặc x = -2 hoặc 5x = 7
<=> x = 1 hoặc x = -2 hoặc x = 7/5
19 tháng 8 2021
1: Ta có: \(\dfrac{3}{x+2}-\dfrac{x-1}{x^2-4}=\dfrac{2}{x-2}\)
Suy ra: \(3x-6-x+1=2x+4\)
\(\Leftrightarrow2x-5=2x+4\left(vôlý\right)\)
2: Ta có: \(\dfrac{x-5}{2x-3}-\dfrac{x}{2x+3}=\dfrac{1-6x}{4x^2-9}\)
Suy ra: \(\left(x-5\right)\left(2x+3\right)-x\left(2x-3\right)=1-6x\)
\(\Leftrightarrow2x^2-7x-15-2x^2+6x+6x-1=0\)
\(\Leftrightarrow5x=16\)
hay \(x=\dfrac{16}{5}\)
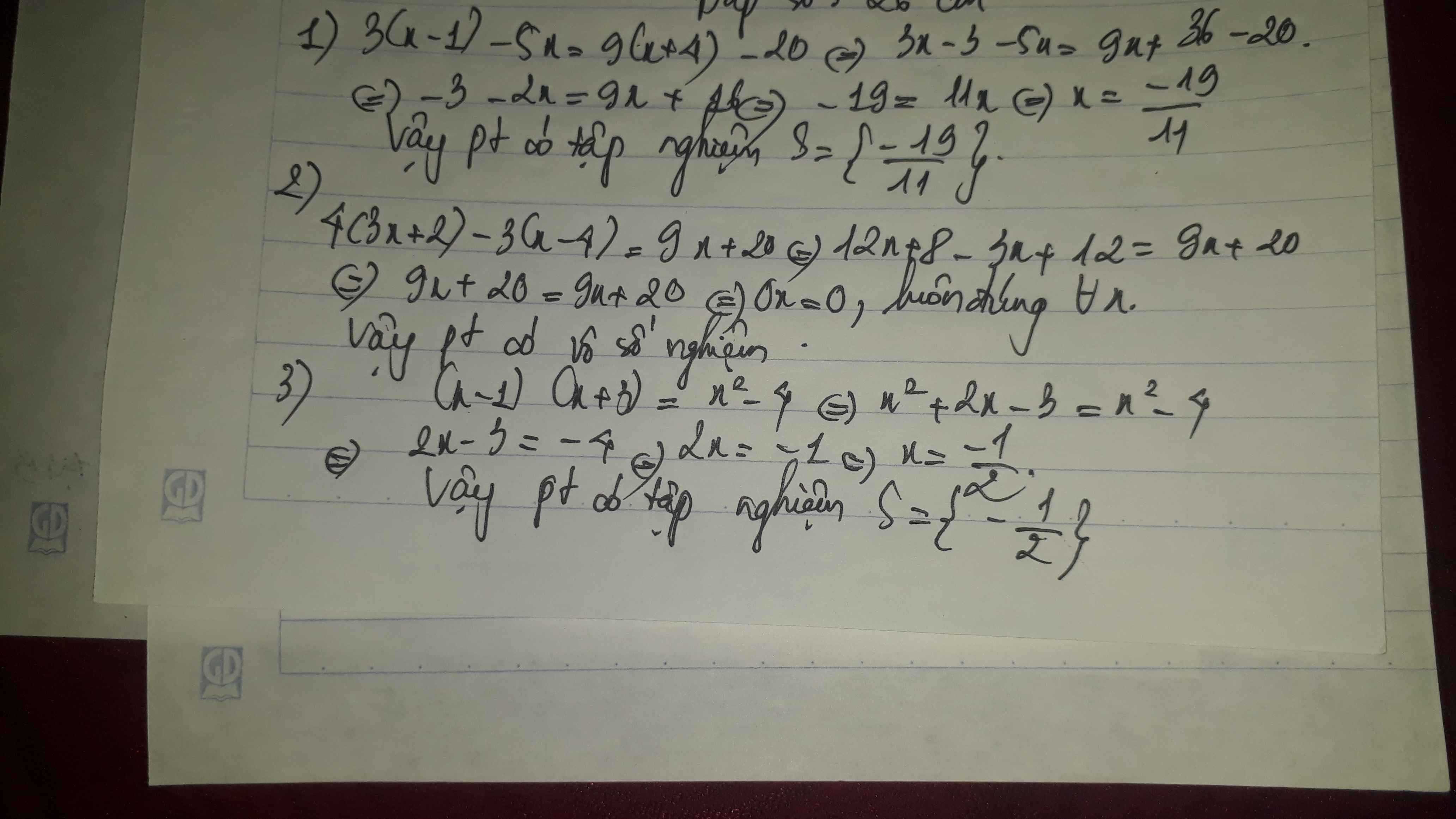
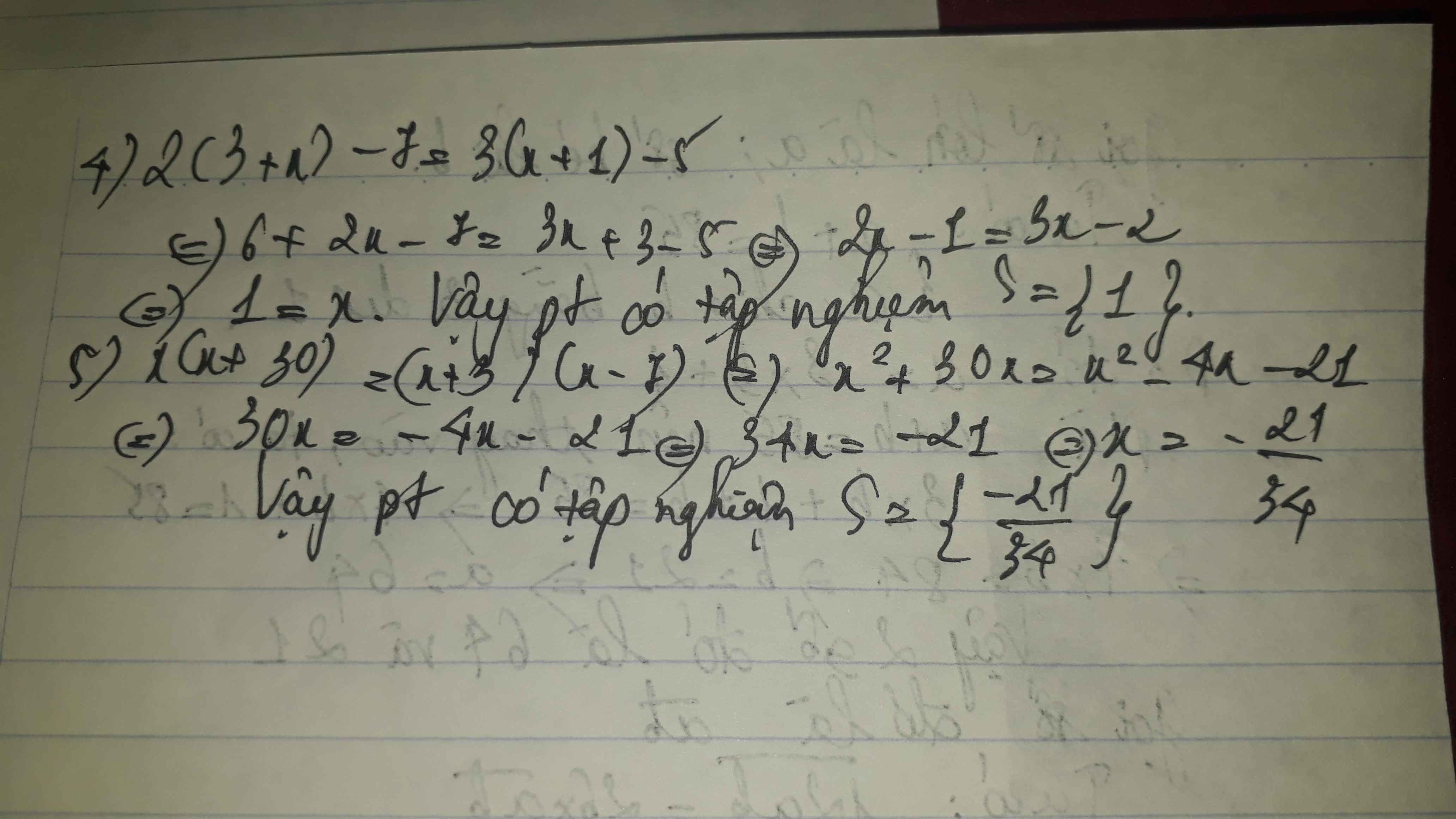
( 9 x 2 – 4 ) ( x + 1 ) = ( 3 x + 2 ) ( x 2 - 1 )
⇔ (3x – 2)(3x + 2)(x + 1) - (3x + 2)(x - 1)(x + 1) = 0
⇔(3x+ 2)(x + 1)(3x – 2 – x + 1) = 0
⇔ (3x + 2)(x + 1)(2x – 1) = 0