Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ĐKXĐ: 2x + 3 ≥ 0. Bình phương hai vế thì được:
(3x – 2)2 = (2x + 3)2 => (3x - 2)2 – (2x + 3)2 = 0
⇔ (3x -2 + 2x + 3)(3x – 2 – 2x – 3) = 0
=> x1 = (nhận), x2 = 5 (nhận)
Tập nghiệm S = {; 5}.
b) Bình phương hai vế:
(2x – 1)2 = (5x + 2)2 => (2x - 1 + 5x + 2)(2x – 1 – 5x – 2) = 0
=> x1 = , x2 = -1.
c) ĐKXĐ: x ≠ , x ≠ -1. Quy đồng rồi khử mẫu thức chung
(x – 1)|x + 1| = (2x – 3)(-3x + 1)
- Với x ≥ -1 ta được: x2 – 1 = -6x2 + 11x – 3 => x1 =
;
x2 =.
- Với x < -1 ta được: -x2 + 1 = -6x2 + 11x – 3 => x1 =
(loại vì không thỏa mãn đk x < -1); x2 =
(loại vì x > -1)
Kết luận: Tập nghiệm S = {;
}
d) ĐKXĐ: x2 +5x +1 > 0
- Với x ≥
ta được: 2x + 5 = x2 + 5x + 1
=> x1 = -4 (loại); x2 = 1 (nhận) - Với x <
ta được: -2x – 5 = x2 + 5x + 1
=> x1 =-6 (nhận); x2 = -1 (loại).
Kết luận: Tập nghiệm S = {1; -6}.

|3x+4)/(x-2)| <=3
<=>|3 +10/(x-2) | <=3
10/(x-2) =t
<=> |3+t| <=3
9 +6t +t^2 <=9 <=> -6<=t <=0
10/(x-2) <=0 => x<2
10/(x-2) >=-6 <=>5/(x-2)>=-3
<=>5 <=-3(x-2) <=>3x <=10-5 =5 => x <=5/3
kết luận x<= 5/3
a) \(\left|\frac{3x+4}{x-2}\right|< =3̸\) đk: x\(\ne\) 2
BPT \(\Leftrightarrow\) \(\left\{{}\begin{matrix}\frac{3x+4}{x-2}\ge-3\\\frac{3x+4}{x-2}\le3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\frac{3x+4}{x-2}+3\ge0\\\frac{3x+4}{x-2}-3\le0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}\frac{6x-2}{x-2}\ge0\\\frac{10}{x-2}\le0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le\frac{1}{3}\\x>2\end{matrix}\right.\\x< 2\end{matrix}\right.\Rightarrow}x\le\frac{1}{3}}\)
b) \(\left|\frac{2x-1}{x-3}\right|\ge1\) đk: x\(\ne\) 3
BPT \(\Leftrightarrow\left[{}\begin{matrix}\frac{2x-3}{x-3}\le-1\\\frac{2x-3}{x-3}\ge1\end{matrix}\right.\)
ta có:
+) \(\frac{2x-3}{x-3}\le-1\Leftrightarrow\frac{2x-3}{x-3}+1\le0\Leftrightarrow\frac{3x-6}{x-3}\le0\Leftrightarrow2\le x< 3\)
+) \(\frac{2x-3}{x-3}\ge1\Leftrightarrow\frac{2x-3}{x-3}-1\ge0\Leftrightarrow\frac{x}{x-3}\ge0\Leftrightarrow\left[{}\begin{matrix}x\le0\\x>3\end{matrix}\right.\)
vậy tập nghiệm là: \((-\infty;0]\cup[2;3)\cup(3;+\infty)\)

e: =>-3<5x-12<3
=>9<5x<15
=>9/5<x<3
f: =>3x+15>=3 hoặc 3x+15<=-3
=>3x>=-12 hoặc 3x<=-18
=>x<=-6 hoặc x>=-4
b: =>(2x-7)(x-5)<=0
=>7/2<=x<=5

lời giải
a) \(\left\{{}\begin{matrix}-2x+\dfrac{3}{5}>\dfrac{2x-7}{3}\left(1\right)\\x-\dfrac{1}{2}< \dfrac{5\left(3x-1\right)}{2}\left(2\right)\end{matrix}\right.\)
(1)\(\Leftrightarrow\)
\(\dfrac{3}{5}+\dfrac{7}{3}>\left(\dfrac{2}{3}+2\right)x\)
\(\dfrac{44}{15}>\dfrac{8}{3}x\) \(\Rightarrow x< \dfrac{44.3}{15.8}=\dfrac{11}{5.2}=\dfrac{11}{10}\)
Nghiêm BPT(1) là \(x< \dfrac{11}{10}\)
(2) \(\Leftrightarrow2x-1< 15x-5\Rightarrow13x>4\Rightarrow x>\dfrac{4}{13}\)
Ta có: \(\dfrac{4}{13}< \dfrac{11}{10}\) => Nghiệm hệ (a) là \(\dfrac{4}{13}< x< \dfrac{11}{10}\)

a)
\(\left\{{}\begin{matrix}x^2\ge\dfrac{1}{4}\left(1\right)\\x^2-x\le0\left(2\right)\end{matrix}\right.\)
\(\left(1\right)x^2-0,25\Leftrightarrow\left[{}\begin{matrix}x\le-\dfrac{1}{2}\\x\ge\dfrac{1}{2}\end{matrix}\right.\)
(2)\(x^2-x\le\) \(\Leftrightarrow0\le x\le1\)
Kết hợp (1) và (2) \(\Rightarrow\dfrac{1}{2}\le x\le1\)
b)
\(\left\{{}\begin{matrix}\left(x-1\right)\left(2x+3\right)>0\left(1\right)\\\left(x-4\right)\left(x+\dfrac{1}{4}\right)\le0\left(2\right)\end{matrix}\right.\)
Giải: \(\left(1\right)\left(x-1\right)\left(2x+3\right)>0\Leftrightarrow\left[{}\begin{matrix}x< -\dfrac{3}{2}\\x>1\end{matrix}\right.\)
Giải: (2) \(\left(x-4\right)\left(x+\dfrac{1}{4}\right)< 0\Leftrightarrow-\dfrac{1}{4}\le x\le4\)
Kết hợp điều kiện của (1) và (2) ta có: (1;4] là nghiệm của hệ bất phương trình.

a)
<=> f(x) = .
Xét dấu của f(x) ta được tập nghiệm của bất phương trình:
T = ∪ [3; +∞).
b)
<=> f(x) = =
.
f(x) không xác định với x = ± 1.
Xét dấu của f(x) cho tập nghiệm của bất phương trình:
T = (-∞; - 1) ∪ (0; 1) ∪ (1; 3).
c) <=> f(x) =
= .
Tập nghiệm: \(\left(-12;-4\right)\cup\left(-3;0\right)\).

a,\(\left\{{}\begin{matrix}-7x+3y=-5\\5x-2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-14x+6y=-10\\15x+6y=12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\5x-2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
\(\Leftrightarrow2x-y=3\)
b,\(\left\{{}\begin{matrix}4x-2y=6\\-2x+y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y=3\\2x-y=3\end{matrix}\right.\Leftrightarrow2x-y=3\)
Vậy hệ phương trình có vô số nghiệm (x;y)= (a;2a-3), a tùy ý
c, \(\left\{{}\begin{matrix}-0,5x+0,4y=0,7\\0,3x-0,2y=0,4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-0,5x+0,4y=0,7\\0,6x-0,4y=0,8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=15\\0,3x-0,2y=0,4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=15\\y=20,5\end{matrix}\right.\)
d, \(\left\{{}\begin{matrix}\dfrac{3}{5}x-\dfrac{4}{3}y=\dfrac{2}{5}\\-\dfrac{2}{3}x-\dfrac{5}{9}y=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{5}x-\dfrac{4}{3}y=\dfrac{2}{5}\\-\dfrac{3}{5}x-\dfrac{1}{2}y=\dfrac{6}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{11}{6}y=\dfrac{8}{5}\\\dfrac{3}{5}x-\dfrac{4}{3}y=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{14}{11}\\y=-\dfrac{48}{55}\end{matrix}\right.\)
a, \(\left|5x-4\right|\ge6\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-4\ge6\\5x-4\le-6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge2\\x\le-\dfrac{2}{5}\end{matrix}\right.\)
a) <=> (5x - 2)2 ≥ 62 <=> (5x – 4)2 – 62 ≥ 0
<=> (5x - 4 + 6)(5x - 4 - 6) ≥ 0 <=> (5x + 2)(5x - 10) ≥ 0
Bảng xét dấu:
Từ bảng xét dấu cho tập nghiệm của bất phương trình:
T = ∪ [2; +∞).
∪ [2; +∞).
b) <=>
<=> 
<=>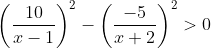
<=>
<=>
Tập nghiệm của bất phương trình T = (-∞; - 5) ∪ (- 1; 1) ∪ (1; +∞).