Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo:
Thông tin trên không đủ để ta xác định độ cao của máy bay so với mặt đất phẳng, tại thời điểm 1 phút kể từ khi máy bay cất cánh mà chỉ tính được quãng đường bay của máy bay bay được.

Sau 1 phút cả 2 máy bay bay được quãng đường dài \(1.v = v\)
Áp dụng công thức tính độ cao của máy bay so với mặt đất, ta tính được độ cao của hai máy bay 1 và 2 như sau:
Độ cao của máy bay 1: \({h_1} = v.\sin {10^0} \approx 0,17v\)
Độ cao của máy bay 2: \({h_2} = v.\sin {15^0} \approx 0,26v\)
Do đó, ta thấy rằng độ cao của máy bay 2 lớn hơn độ cao của máy bay 1. Vì vậy, máy bay 2 ở độ cao so với mặt đất lớn hơn sau 1 phút kể từ khi cất cánh.

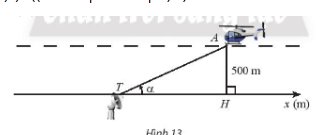
a, Xét tam giác AHT vuông tại H, ta có:
\(cot\alpha=\dfrac{TH}{AH}\Rightarrow TH=AH\cdot cot\alpha=500\cdot cot\alpha\)
Vậy trên trục \(T_x\) tọa độ \(x_H=500\cdot cot\alpha\)
b, Ta có đồ thị của hàm số \(y=cot\alpha\) trong khoảng \(\dfrac{\pi}{6}< \alpha< \dfrac{2\pi}{3}\)
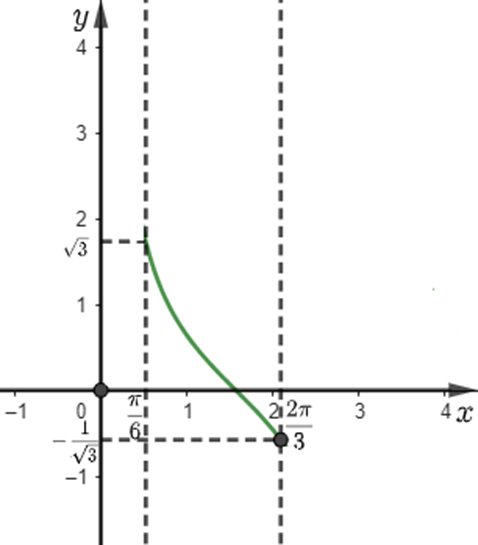
Khi đó:
\(-\dfrac{1}{\sqrt{3}}< cot\alpha< \dfrac{1}{\sqrt{3}}\Leftrightarrow-\dfrac{500}{\sqrt{3}}< 500\cdot cot\alpha< \dfrac{500}{\sqrt{3}}\\ \Leftrightarrow-\dfrac{500}{\sqrt{3}}< x_H< \dfrac{500}{\sqrt{3}}\\ \Leftrightarrow-288,7< x_H< 866\)
Vậy \(x\in\left\{-288,7;866\right\}\)

Ta có: \(v\left(t\right)=h'\left(t\right)=-9,8t\)
a, Vận tốc của vật tại thời điểm t = 5s là \(v\left(5\right)=-9,8\cdot5=-49\left(m/s\right)\)
b, Khi vật chạm đất thì \(h\left(t\right)=100-4,9t^2=0 \Rightarrow t=\dfrac{10\sqrt{10}}{7}\left(s\right)\)
Khi đó, vận tốc vật chạm đất là: \(v\left(\dfrac{10\sqrt{10}}{7}\right)=-9,8\cdot\dfrac{10\sqrt{10}}{7}=-14\sqrt{10}\left(m/s\right)\)

Với \({x_0}\) bất kì, ta có:
\(f'\left( {{t_0}} \right) = \mathop {\lim }\limits_{t \to {t_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{19,6t - 4,9{t^2} - 19,6{t_0} + 4,9t_0^2}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to {t_0}} \frac{{ - 4,9\left( {{t^2} - t_0^2} \right) + 19,6\left( {t - {t_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to {t_0}} \frac{{\left( {t - {t_0}} \right)\left( { - 4,9t - 4,9{t_0} + 19,6} \right)}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to {t_0}} \left( { - 4,9t - 4,9{t_0} + 19,6} \right) = - 9,8{t_0} + 19,6\)
Vậy hàm số \(h = 19,6t - 4,9{t^2}\) có đạo hàm là hàm số \(h' = - 9,8{t_0} + 19,6\)
Độ cao của vật khi nó chạm đất thỏa mãn \(19,6t - 4,9{t^2} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 4\end{array} \right.\)
Khi t = 4, vận tốc của vật khi nó chạm đất là \( - 9,8.4 + 19,6 = - 19,6\) (m/s)
Vậy vận tốc của vật khi nó chạm đất là 19,6 m/s.

a, Ta có:
\(48=16+32\\ 80=48+32\\ 112=80+32\\ 144=112+32\\ ...\)
Vậy dãy số trên là cấp số cộng có số hạng đầu \(u_1=16\) và công sai \(d=32\)
b, Tổng chiều dài quãng đường rơi tự do của người đó trong 10s đầu tiên là:
\(S_{10}=\dfrac{10\cdot\left[u_1+\left(10-1\right)d\right]}{2}=\dfrac{10\cdot\left[2u_1+9d\right]}{2}=\dfrac{10\cdot\left(2\cdot16+9\cdot32\right)}{2}=1600\left(feet\right)\)

Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng 1/10 độ cao của lần rơi ngay trước đó và sau đó lại rơi xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:
- Thời điểm chạm đất lần thứ nhất là d 1 = 63
- Thời điểm chạm đất lần thứ hai là:
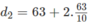
- Thời điểm chạm đất lần thứ ba là:
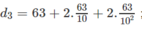
- Thời điểm chạm đất lần thứ tư là:
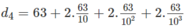
....
- Thời điểm chạm đất lần thứ n (n > 1) là
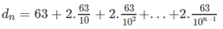
(Có thể chứng minh khẳng định này bằng quy nạp).
Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến khi nằm yên trên mặt đất là :
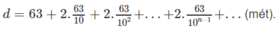
Vì 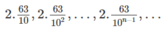
là một cấp số nhân lùi vô hạn, công bội q = 1/10 nên ta có
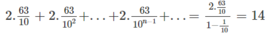
Vậy
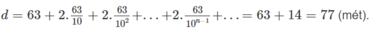

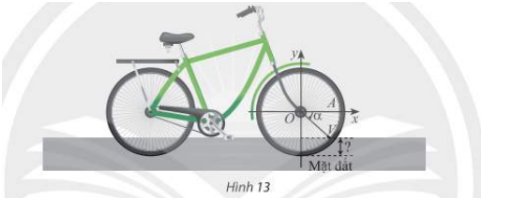
Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha=11\cdot60=660\left(rad\right)\)
Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left(58\cdot cos\alpha,58\cdot sin\alpha\right)\approx\left(56;15,2\right)\)
Từ đó, khoảng cách từ van đến mặt đất khoảng \(58-15,2\approx42,8\left(cm\right)\)



Đổi \(200km/h = \frac{{500}}{9}m/s\)
Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.
Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)
Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:
\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)
Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.