Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số con gà
\(\Rightarrow x-6\) là số con lợn
Theo đề bài ta có
\(2x+6=4\left(x-6\right)\)
\(\Leftrightarrow2x+6-4\left(x-6\right)=0\)
\(\Leftrightarrow2x+6-4x+24=0\)
\(\Leftrightarrow-2x+30=0\Leftrightarrow-2x=-30\Leftrightarrow x=15\)
Vậy có 15 con gà
Số con lợn \(x-6=15-6=9\)
Vậy có 15 con gà và 9 con lợn

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

Gọi số trâu đứng là x;trâu nằm là y; trâu già là z
Theo đề bài ta có hệ
x+y+z=100 (1)
5x+3y+1/3z=100 (2)
x,y,z thuộc N,x,y,z>=1
Thế z ở (1) vào (2) ta có pt
7x+4y=100
Vì 4 và 100 đều chia hết cho 4 nên để hệ có nghiệm nguyên thì x chia hết cho 4
Đặt x=4m ta có y = 25-7m
Vì x,y>=1 nên 1<=m<=3
Với m=1 => x=4;y=18;z=78
Với m= 2 ta có x=8;y=11;z=81
Với m=3 ta có x=12 ; y=4 ; z=84
Số trâu mỗi loại là:
Đáp án 1: Trâu đứng 4, trâu nằm 18, trâu già 78.
Đáp án 2: Trâu đứng 8, trâu nằm 11, trâu già 81.
Đáp án 3: Trâu đứng 12, trâu nằm 4, trâu già 84.
hỏi pt là vậy còn mẹo thì mik ko có bik nha bạn
chỗ này mk k hiểu cho lắm giải htichs lại cho mk nha:
x,y,z thuộc N,x,y,z>=1
Thế z ở (1) vào (2) ta có pt
7x+4y=100
Vì 4 và 100 đều chi hết cho 4 nên để hệ có nghiệm nguyên thì x chia hết cho 4
Đặt x=4m ta có y = 25-7m
Vì x,y>=1 nên 1<=m<=3

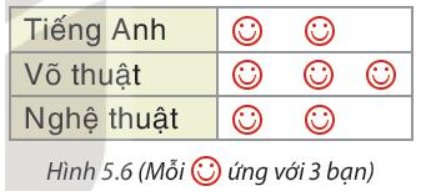
a: Biểu đồ đã cho là biểu đồ tranh
Mỗi biểu tượng ứng với 3 hs
b: Bảng thống kê:
| Tên CLB | Tiếng Anh | Võ thuật | Nghệ thuật |
| Số lượng | 6 | 9 | 6 |

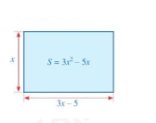
\(3{{\rm{x}}^2} - 5{\rm{x = x}}\left( {3{\rm{x}} - 5} \right)\)

con đứng:12 con con nằm :4 con con già :84 con
tick nha

35 nhưng mình không biết cách làm trong cuộc thi MYTS có câu này

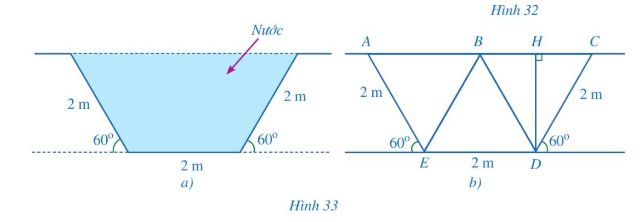
a, Do ACDE là hình thang cân nên
AC//DE suy ra AB//ED \( \Rightarrow {{\widehat B} _1} = {{\widehat E} _3},{{\widehat A} _1} = {{\widehat E} _1} = {60^0};{{\widehat C} _1} = {{\widehat D} _1} = {60^0}\)
Mà: AE//BD \( \Rightarrow {{\widehat B} _2} = {{\widehat E} _2}\)
Xét \(\Delta ABE\) và \(\Delta B{\rm{D}}E\) có: \({{\widehat B} _1} = {{\widehat E} _3}\) ; BE chung
\(\begin{array}{l}{{{\widehat B} }_2} = {{{\widehat E} }_2} \Rightarrow \Delta ABE = \Delta B{\rm{D}}E \Rightarrow A{\rm{E}} = B{\rm{D}} = 2m.\\AB = E{\rm{D}} = 2m\end{array}\)
Xét \(\Delta BC{\rm{D}}\) có \({{\widehat C} _1} = {60^0};B{\rm{D}} = C{\rm{D}} = 2m \Rightarrow \Delta BC{\rm{D}}\) đều.
Xét \(\Delta A{\rm{E}}B\) có \({{\widehat A} _1} = {60^0};AB = A{\rm{E}} = 2m \Rightarrow \Delta A{\rm{E}}B\) đều.
Vì: \(\Delta A{\rm{E}}B\) đều suy ra: BE = 2 m.
Xét \(\Delta BE{\rm{D}}\) có BD = BE = ED = 2m \( \Rightarrow \Delta BE{\rm{D}}\) đều.
b, Vì \(\Delta ABE,\Delta BC{\rm{D}}\) là các tam giác đều nên AB = BC = 2m.
Suy ra AC = AB + BC = 4m.
Do \(\Delta B{\rm{D}}C\) đều nên H là trung điểm của BC.
Suy ra HC = HB =\(\dfrac{{BC}}{2} = 1\)
Xét \(\Delta DHC\) vuông tại H ta có:
\(D{C^2} = D{H^2} + H{C^2}\) (theo định lý pythagore)
\(\begin{array}{l} \Rightarrow D{H^2} = D{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow DH = \sqrt 3 \end{array}\)
c, Diện tích hình thang cân AEDC là:
\({S_{A{\rm{ED}}C}} = \dfrac{1}{2}DH.(AC + E{\rm{D}}) = \dfrac{1}{2}\sqrt 3 (2 + 4) = 3\sqrt 3 (c{m^2})\)
Vậy diện tích mặt cắt phần chứa nước: \(3\sqrt 3 c{m^2}\)



Con lợn thứ nhất ăn 3 ngày ăn hết 1 bao thức ăn
Suy ra một ngày con lợn thứ nhất ăn hết \(\dfrac{1}{3}\) bao thức ăn
Con lợn thứ hai ăn 6 ngày ăn hết 1 bao thức ăn
Suy ra một ngày con lợn thứ hai ăn hết \(\dfrac{1}{6}\) bao thức ăn
Con lợn thứ ba ăn 4 ngày ăn hết 1 bao thức ăn
Suy ra một ngày con lợn thứ ba ăn hết \(\dfrac{1}{4}\) bao thức ăn
Một ngày ba con lợn ăn hết: \(\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{4} = \dfrac{3}{4}\) (bao thức ăn)
Cả ba con lợn trong x (ngày) cần số bao thức ăn là: \(\dfrac{3}{4}x\) (bao thức ăn)