Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 5cm và \(\widehat{B}=35^0\) ?

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

SG

Sách Giáo Khoa

28 tháng 4 2017

Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 5cm và \(\widehat{B}=35^0\) ?

1

NT

Nguyen Thuy Hoa

29 tháng 6 2017

Dựng hình bằng thước và compa. Dựng hình thang

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

21 tháng 4 2017

Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn \(\widehat{B}=65^0\)

1

H

Hiiiii~

21 tháng 4 2017

Bài giải:

Sử dụng phương pháp dựng tam giác vuông đã được học.

Ta lần lượt thực hiên:

- Vẽ đoạn BC = 4cm.

- Vẽ tia Bx tạo với BC một góc 65⁰

- Vẽ đường thẳng a qua C và vuông góc với Bx và cắt Bx tại A.

Khi đó ∆ABC là tam giác cần dựng.

PT

Pham Trong Bach

13 tháng 2 2017

Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 5cm, B = 35 0

1

CM

Cao Minh Tâm

13 tháng 2 2017

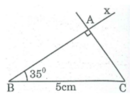
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Cách dựng:

- Dựng đoạn BC = 5cm

- Dựng góc ∠ CBx = 35 0

- Dựng CA ⊥ Bx ta có ∆ ABC dựng được.

Chứng minh: ∆ ABC có ∠ A = 90o, ∠ B = 35 0 , BC = 5cm. Thỏa mãn điều kiện bài toán.

SG

Sách Giáo Khoa

28 tháng 4 2017

Dựng tam giác ABC biết \(\widehat{B}=80^0;BC=3cm,AB+AC=5cm\)

2

C

Cheewin

28 tháng 4 2017

A B C D

NT

Nguyen Thuy Hoa

29 tháng 6 2017

Dựng hình bằng thước và compa. Dựng hình thang

PT

Pham Trong Bach

16 tháng 7 2018

Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4,5cm và cạnh góc vuông AC = 2cm

1

CM

Cao Minh Tâm

16 tháng 7 2018

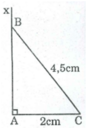
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Cách dựng:

- Dựng đoạn AC = 2cm.

- Dựng góc ∠ (CAx) bằng 90 0

- Dựng cung tròn tâm C bán kính 4,5cm cắt Ax tại B. Nối CB ta có ΔABC cần dựng .

Chứng minh:

∆ ABC có ∠ A = 90 0 , AC = 2 cm, BC = 4,5 cm.

Thỏa mãn điều kiện bài toán.

SG

Sách Giáo Khoa

28 tháng 4 2017

Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4,5cm và cạnh góc vuông AC = 2cm ?

1

TC

Tuyen Cao

9 tháng 8 2017

A C B 4,5 cm 2 cm

SG

Sách Giáo Khoa

21 tháng 4 2017

Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4m, cạnh góc vuông BC = 2cm

1

H

Hiiiii~

21 tháng 4 2017

Bài giải:

Sử dụng phương pháp dựng phương pháp vuông đã được học.

Ta lần lượt thực hiện:

- Vẽ góc vuông xBy. Trên tia Bx lấy điểm C sao cho BC = 2cm.

- Vẽ đường tròn (C; 4) và đường tròn này cắt tia Oy tại A.

Nối A với C ta được ∆ABC là tam giác cần dựng.

TT

Trần Tuyết Như

25 tháng 7 2015 - olm

Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.

3

MT

Minh Triều

25 tháng 7 2015

giả sử ta đã có tam giác ABC vuông tại B

áp dụng định lí py-ta-go vào tam giác ABC vuông tại B có:

BC²+AB²=AC²

2²+AB²=4²

4+AB²=16

AB²=12

=>AB=\(\sqrt{12}\)(cm)

Các bước vẽ :

B₁: vẽ đoạn thẳng AC = 4cm

B₂: dùng com-pa vẽ một đường tròn tâm A bán kính 2 cm

B₃: dùng com-pa vẽ một đường tròn tâm AB bán kính \(\sqrt{12}cm\)

B₄ : 2 đường tròn cắt nhau tại một điểm điểm đó là B nói 3 điểm A;B;C lại với nhau ta được tam giác ABC vuông tại B có cạnh huyền AC=4cm cạnh góc vuông BC=2cm

TT

Trần Tuyết Như

25 tháng 7 2015

bài này cần 4 bước:

- Phân tích

- dựng hình

- chứng minh

-biện luận

ST

Soái Tỷ Trời Đẹp

11 tháng 4 2018 - olm

Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn ˆBB^=65⁰

3

P

Premis

11 tháng 4 2018

Bài giải:

Sử dụng phương pháp dựng tam giác vuông đã được học.

Học sinh tự vẽ hình

Ta lần lượt thực hiên:

- Vẽ đoạn BC = 4cm.

- Vẽ tia Bx tạo với BC một góc 65⁰

- Vẽ đường thẳng a qua C và vuông góc với Bx và cắt Bx tại A.

Khi đó ∆ABC là tam giác cần dựng.

P

phuong

11 tháng 4 2018

Ta lần lượt thực hiên:

– Vẽ đoạn BC = 4cm.

– Vẽ tia Bx tạo với BC một góc 650

– Vẽ đường thẳng a qua C và vuông góc với Bx và cắt Bx tại A.

Khi đó ∆ABC là tam giác cần dựng.

PT

Pham Trong Bach

6 tháng 9 2018

Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn B = 65o.

1

CM

Cao Minh Tâm

6 tháng 9 2018

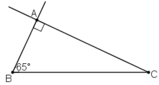
Giải bài 29 trang 83 Toán 8 Tập 1 | Giải bài tập Toán 8

a) Phân tích

Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.

Đoạn thẳng BC dựng được vì đã biết độ dài.

Khi đó điểm A là giao điểm của:

+ Tia Bx tạo với đoạn thẳng BC góc 65º

+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.

b) Cách dựng:

- Dựng đoạn thẳng BC = 4cm.

- Dựng tia Bx tạo với BC một góc 65º.

- Dựng đường thẳng a qua C và vuông góc với Bx.

- Bx cắt a tại A.

ΔABC là tam giác cần dựng.

c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.

d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.