Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tính chất trên gọi là tính chất bắc cầu, ta so sánh hai phân số với một số (phân số) thứ 3.

a) \(\frac{6}{7}\) và \(\frac{11}{10}\)
\(\frac{6}{7}< 1\)
\(\frac{11}{10}>1\)
\(\Rightarrow\frac{6}{7}< 1< \frac{11}{10}\Rightarrow\frac{6}{7}< \frac{11}{10}\)
b) \(\frac{-5}{17}\) và \(\frac{2}{7}\)
\(\frac{-5}{17}< 0\)
\(\frac{2}{7}>0\)
\(\Rightarrow\frac{-5}{17}< 0< \frac{2}{7}\)\(\Rightarrow\frac{-5}{17}< \frac{2}{7}\)
c) \(\frac{419}{-723}\) và \(\frac{-697}{-313}\)
\(\frac{419}{-724}< 0\)
\(\frac{-697}{-313}>0\)
\(\Rightarrow\frac{419}{-724}< 0< \frac{-697}{-313}\Rightarrow\frac{419}{-723}< \frac{-697}{-313}\)

a: \(=\dfrac{-28}{36}+\dfrac{15}{36}-\dfrac{26}{36}=\dfrac{-39}{36}=\dfrac{-13}{12}\)
b: \(=\dfrac{11}{9}\left(\dfrac{15}{4}-\dfrac{7}{4}-\dfrac{5}{4}\right)=\dfrac{11}{9}\cdot\dfrac{3}{4}=\dfrac{11}{12}\)
c: \(=15+\dfrac{9}{7}+6+\dfrac{2}{3}-5-\dfrac{5}{9}\)
\(=16+\dfrac{88}{63}=\dfrac{1096}{63}\)
d: \(=\dfrac{5}{6}-\dfrac{1}{3}+\dfrac{2}{18}\)
\(=\dfrac{15-6+2}{18}=\dfrac{11}{18}\)

A=\(\dfrac{2}{7}+\dfrac{-3}{8}+\dfrac{11}{7}+\dfrac{1}{3}+\dfrac{1}{7}+\dfrac{5}{-3}\)
A=\(\left(\dfrac{2}{7}+\dfrac{11}{7}+\dfrac{1}{7}\right)+\left(\dfrac{1}{3}+\dfrac{5}{-3}\right)+\dfrac{-3}{8}\)
A=\(2+\dfrac{-4}{3}+\dfrac{-3}{8}\)
A=\(\dfrac{7}{24}\)
B=\(\left(\dfrac{3}{17}+\dfrac{14}{17}\right)+\left(\dfrac{-18}{35}+\dfrac{17}{-35}\right)+\left(\dfrac{-5}{13}+\dfrac{-8}{13}\right)\)
B=\(\dfrac{17}{17}+\dfrac{-35}{35}+\dfrac{-13}{13}\)
B=\(1+\left(-1\right)+\left(-1\right)=-1\)
C=\(\dfrac{-3}{17}+\left(\dfrac{2}{3}+\dfrac{3}{17}\right)\)
C=\(\dfrac{-3}{17}+\dfrac{2}{3}+\dfrac{3}{17}=\left(\dfrac{-3}{17}+\dfrac{3}{17}\right)+\dfrac{2}{3}\)
C=0+\(\dfrac{2}{3}=\dfrac{2}{3}\)
D=\(\left(\dfrac{-1}{6}+\dfrac{5}{-12}\right)+\dfrac{7}{12}\)
D=\(\dfrac{-1}{6}+\dfrac{5}{-12}+\dfrac{7}{12}\)
D=\(\dfrac{-2}{12}+\dfrac{-5}{12}+\dfrac{7}{12}=\left(\dfrac{-2}{12}+\dfrac{-5}{12}\right)+\dfrac{7}{12}\)
D=\(\dfrac{-7}{12}+\dfrac{7}{12}=0\)

a)
\(3\dfrac{14}{19}+\dfrac{13}{17}+\dfrac{35}{43}+6\dfrac{5}{19}+\dfrac{8}{43}\\ =\left(3\dfrac{14}{19}+6\dfrac{5}{19}\right)+\left(\dfrac{35}{43}+\dfrac{8}{43}\right)+\dfrac{13}{17}\\ =10+1+\dfrac{13}{17}\\ =11\dfrac{13}{17}\)
b)
\(\dfrac{-5}{7}\cdot\dfrac{2}{11}+\dfrac{-5}{7}\cdot\dfrac{9}{11}+1\dfrac{5}{7}\\ =\dfrac{-5}{7}\cdot\left(\dfrac{2}{11}+\dfrac{9}{11}\right)+1\dfrac{5}{7}\\ =\dfrac{-5}{7}\cdot1+1\dfrac{5}{7}\\ =\dfrac{-5}{7}+1\dfrac{5}{7}\\ =1\)
a) \(3\dfrac{14}{19}+\dfrac{13}{17}+\dfrac{35}{43}+6\dfrac{5}{19}+\dfrac{8}{43}\)
\(=\left(3\dfrac{14}{19}+6\dfrac{5}{19}\right)+\left(\dfrac{35}{43}+\dfrac{8}{43}\right)+\dfrac{13}{17}\)
\(=\left[\left(3+6\right)+\left(\dfrac{14}{19}+\dfrac{5}{19}\right)\right]+1+\dfrac{13}{17}\)
\(=\left[9+1\right]+1+\dfrac{13}{17}\)
\(=10+1+\dfrac{13}{17}\)
\(=11+\dfrac{13}{17}\)
\(=\dfrac{187}{17}+\dfrac{13}{17}\)
\(=\dfrac{200}{17}\)
b) \(\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{7}.\dfrac{9}{11}+1\dfrac{5}{7}\)
\(=\dfrac{-5}{7}.\left(\dfrac{2}{11}+\dfrac{9}{11}\right)+\dfrac{12}{7}\)
\(=\dfrac{-5}{7}.1+\dfrac{12}{7}\)
\(=\dfrac{-5}{7}+\dfrac{12}{7}\)
\(=\dfrac{7}{7}\)
\(=1\)
c) \(11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)
= \(11\dfrac{3}{13}-2\dfrac{4}{7}-5\dfrac{3}{13}\)
\(=\left(11\dfrac{3}{13}-5\dfrac{3}{13}\right)-2\dfrac{4}{7}\)
\(=\left[\left(11-5\right)+\left(\dfrac{3}{13}-\dfrac{3}{13}\right)\right]-\dfrac{18}{7}\)
\(=\left[6+0\right]-\dfrac{18}{7}\)
\(=6-\dfrac{18}{7}\)
\(=\dfrac{42}{7}-\dfrac{18}{7}\)
\(=\dfrac{24}{7}\)
d) \(\dfrac{2}{7}.5\dfrac{1}{4}-\dfrac{2}{7}.3\dfrac{1}{4}\)
\(=\dfrac{2}{7}.\left(5\dfrac{1}{4}-3\dfrac{1}{4}\right)\)
\(=\dfrac{2}{7}.\left[\left(5-3\right)+\left(\dfrac{1}{4}-\dfrac{1}{4}\right)\right]\)
\(=\dfrac{2}{7}.\left[2+0\right]\)
\(=\dfrac{2}{7}.2\)
= \(\dfrac{4}{7}\)

a, Ta có :
\(\dfrac{1}{6}< \dfrac{1}{5}\)
\(\dfrac{1}{7}< \dfrac{1}{5}\)
.................
\(\dfrac{1}{9}< \dfrac{1}{5}\)
\(\dfrac{1}{10}=\dfrac{1}{10}\)
\(\dfrac{1}{11}< \dfrac{1}{10}\)
..................
\(\dfrac{1}{17}< \dfrac{1}{10}\)
\(\Leftrightarrow\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+......+\dfrac{1}{17}< \dfrac{1}{5}+\dfrac{1}{5}+....+\dfrac{1}{5}\)
\(\Leftrightarrow A< \dfrac{1}{5}.5+\dfrac{1}{10}.8\)
\(\Leftrightarrow A< 1+\dfrac{4}{5}=\dfrac{9}{5}< 2\)
\(\Leftrightarrow A< 2\left(đpcm\right)\)
b/ Ta có :
\(\dfrac{1}{11}>\dfrac{1}{30}\)
\(\dfrac{1}{12}>\dfrac{1}{30}\)
...............
\(\dfrac{1}{29}>\dfrac{1}{30}\)
\(\dfrac{1}{30}=\dfrac{1}{30}\)
\(\Leftrightarrow\dfrac{1}{11}+\dfrac{1}{12}+........+\dfrac{1}{30}>\dfrac{1}{30}+\dfrac{1}{30}+.......+\dfrac{1}{30}\)
\(\Leftrightarrow B>\dfrac{1}{30}.20=\dfrac{2}{3}\)
\(\Leftrightarrow B>\dfrac{2}{3}\left(đpcm\right)\)

a;\(\dfrac{-6}{11}\) : \(\dfrac{12}{55}\) = \(\dfrac{-5}{2}\)
b;\(\dfrac{7}{12}\) + \(\dfrac{5}{72}\) - \(\dfrac{11}{36}\) = \(\dfrac{47}{72}\) - \(\dfrac{11}{36}\) = \(\dfrac{25}{72}\)
c;\(\dfrac{13}{10}\) : \(\dfrac{-5}{13}\) = \(\dfrac{-169}{50}\)
d; {\(\dfrac{5}{12}\) + \(\dfrac{5}{11}\) } : { \(\dfrac{5}{3}\) -\(\dfrac{7}{11}\) } = \(\dfrac{115}{132}\) : \(\dfrac{34}{33}\) = \(\dfrac{115}{136}\)
lưu ý mk ko chép đầu bài
mình cần gấp lắm đến chiều mai là phải nộp rùi
giúp mình nha thanks cá bạn trước ![]() ko có tâm trạng mà cười nữa
ko có tâm trạng mà cười nữa![]()
![]()
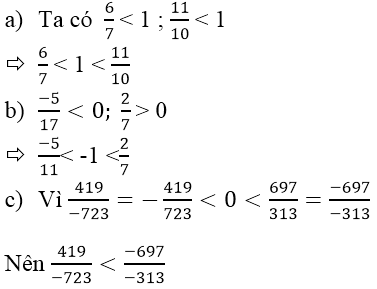
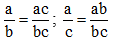

a) \(\left\{{}\begin{matrix}\dfrac{11}{10}>\dfrac{10}{10}\\\dfrac{10}{10}=\dfrac{7}{7}>\dfrac{6}{7}\end{matrix}\right.\) \(\Rightarrow\dfrac{11}{10}>\dfrac{6}{7}\)
b) \(\left\{{}\begin{matrix}\dfrac{2}{7}>\dfrac{0}{7}\\\dfrac{0}{7}=\dfrac{0}{17}>-\dfrac{5}{17}\end{matrix}\right.\) \(\Rightarrow\dfrac{2}{7}>\dfrac{-5}{17}\)
c)
\(\left\{{}\begin{matrix}\dfrac{-697}{-313}=\dfrac{697}{313}>\dfrac{0}{313}\\\dfrac{0}{313}=\dfrac{0}{723}>\dfrac{-419}{723}=\dfrac{419}{-723}\end{matrix}\right.\) \(\Rightarrow\dfrac{-697}{-313}>\dfrac{419}{-723}\)
Mk chỉ cho gợi ý thôi nha.
Cũng không khó lắm nên bạn có thể tự làm mà.
a) So sánh với 1
b) So sánh với 0
c) So sánh với 0
Chúc bạn học tốt!