Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Điều kiện \(n+2\ne0\Leftrightarrow n\ne-2\)
b) \(E=\frac{3n+7}{n+2}=\frac{3n+6+1}{n=2}=\frac{3\left(n+2\right)}{n+2}+\frac{1}{n+2}=3+\frac{1}{n+2}\)
Để E thuộc Z thì 1 phải chia hết cho n+2 hay n+2 là ước của 1
Ư(1) = {-1; 1}
+) n+2 = -1 => n = -3
+) n+2 = 1 => n = -1
Vậy n E {-3; -1} thì E thuộc Z

Đặt A= như đã cho.
Để AEZ =>n+7 chia hết cho n-2.
=>n-2+9 chia hết cho n-2.
Mà n-2 chia hết cho n-2.
=>9 chia hết cho n-2.
=>n-2E{-9;-3;-1;1;3;9}.
=>nE{-7;-1;1;3;5;11}(tương ứng).
bn thử lại rồi kết luận là được.
tk mk nha các bn.
-chúc ai tk mk hoc jgioir-
Gọi \(\frac{n+7}{n-2}\) là A
\(A=\frac{n+7}{n-2}=\frac{n-2+9}{n-2}\)\(=1+\frac{9}{n-2}\)
Theo đề bài n là ước nguyên dương của 9
\(n-2=1\Rightarrow n=3\)
\(n-2=3\Rightarrow n=5\)
\(n-2=9\Rightarrow n=11\)
mink nghĩ đề bài phải là \(n\in Z\)thì A mới thuộc Z chứ bạn, nhưng mink theo đề bài làm thế kia, ai thấy đúng thì ủng hộ

-4,2 e Z : đúng
0 e N : đúng
0 e Z : đúng
-1 e N : Sai ( sửa thành 1 e N )
100 e N : đúng
Chúc bạn học tốt

a. Đ ; b.Đ ; c.S ; d.Đ ; e.S ; f.S ; g. Đ ; h.S ; i. S ; j. Đ

Để A là số nguyên thì 3 phải chia hết cho n + 5
=> n + 5 sẽ thuộc Ư(3)
Mà 3 = 1.3 = -1.(-3)
Ta có bảng:
| n + 5 | 1 | 3 | -1 | -3 |
| n | -4 | -2 | -6 | -8 |
Vậy n = -4 hoặc -2 hoặc -6 hoặc -8.
Tik nhá
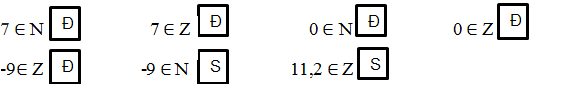
7 E N là đúng
7 E Z là đúng
0 E N là đúng
0 E Z là đúng
-9 E Z là đúng
-9 E N là sai
11, 2 E Z là sai
Đ
Đ
Đ
Đ
Đ
S
Đ