Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Cách đo:
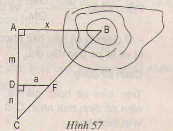
- Chọn thêm hai điểm D và C sao cho A, D, C thẳng hàng và AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thẳng hàng và DF ⊥ AC.
Giải:
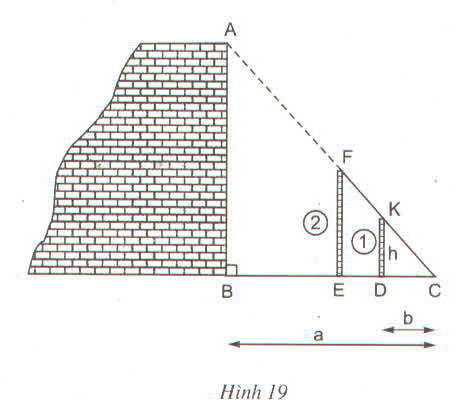
a) Cách đo: Chọn thêm hai điểm C và D sao cho A,D,C thẳng hàng AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thằng hàng và DF ⊥ AC.
b) ∆CDF ∽ ∆CAB (DF // AB)
=> DFAB=CDCADFAB=CDCA = > AB = DF.CACD=a(m+n)mDF.CACD=a(m+n)m
vẫy x= DF.CACD=a(m+n)mDF.CACD=a(m+n)m

Bài giải:
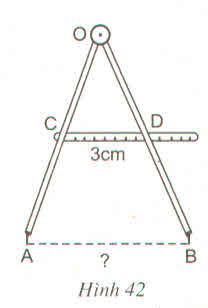
Ta có CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ∆OAB.
Do đó CD = 1212AB
Suy ra AB = 2CD = 2.3 = 6cm.
Ta có: CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ΔOAB
Suy ra AB = 2CD = 2.3 = 6cm

Xét ΔABC có
M là trung điểm của BC
N là trung điểm của AB
Do đó: MN là đường trung bình
=>MN=AC/2
hay AC=50m

- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A,F,K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất( 3 điểm F,K,C thẳng hàng).
b) ∆BC có AB // EF nên EFABEFAB = ECBCECBC => AB = EF.BCECEF.BCEC = h.abh.ab
Vậy chiều cao của bức tường là: AB = h.abh.ab.
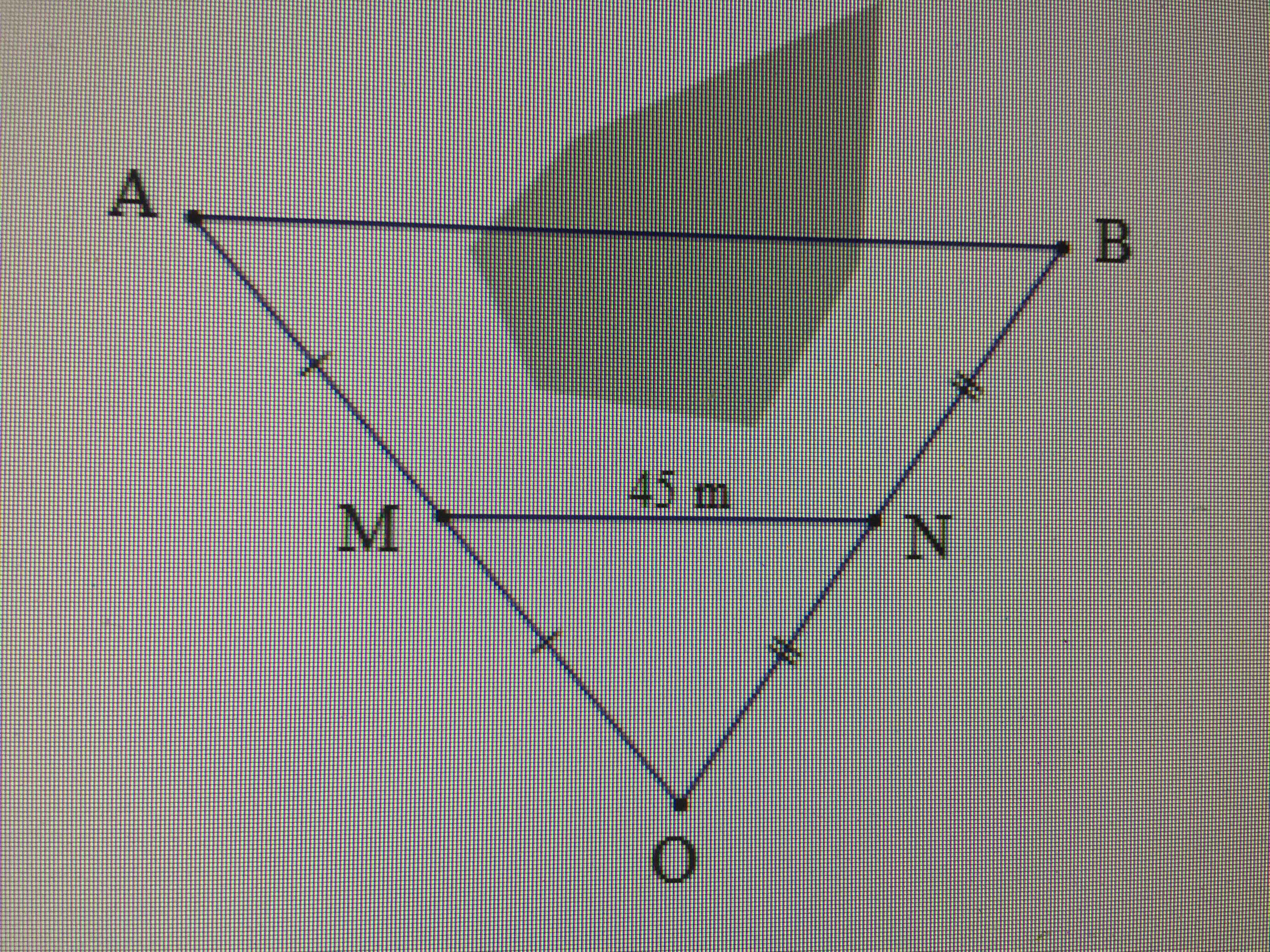
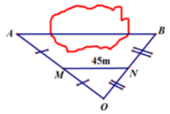


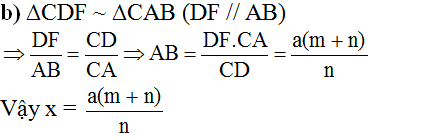

Xét tam giác OAB có:
M là trung điểm AO(gt)
N là trung điểm OB(gt)
=> MN là đường trung bình
\(\Rightarrow AB=2MN=2.45=90\left(m\right)\)