Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng kết quả chuẩn hóa của bài toán ω thay đổi để điện áp hiệu dụng trên tụ điện cực đại, khi đó Z L = 1 Z C = n R = 2 n − 2
→ U L = 0 , 1 U R ⇔ Z L = 0 , 1 R ⇔ 1 = 0 , 1 2 n − 2
→ n = 51
Hệ số công suất của mạch khi đó
cos φ = 2 1 + n = 2 1 + 51 = 1 26
Đáp án D

Giải thích: Đáp án B

Thay vào (1) ta được: 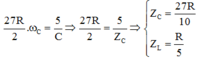
Hệ số công suất của mạch khi đó: 

Đáp án B
+ Khi xảy ra cực đại của điện áp hiệu dụng trên tụ ω = ω C
Ta chuẩn hóa 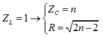
+ Với UR = 5UR → R = 5ZL→ n = 13,5.
→ Hệ số công suất của mạch cos φ = 2 n + 1 = 2 59

Thay đổi ω để điện áp hai đầu tụ điện đạt cực đại, chuẩn hóa
Z L = 1 Z C = n R = 2 n − 2 ⇒ U R = 5 U d ⇔ U 2 n − 2 n 2 − 1 = 5 U n 2 − 1 ⇒ n = 13 , 5
→ Hệ số công suất của đoạn mạch lúc đó cos φ = 2 1 + n = 2 29
Đáp án B

Thay đổi ω để điện áp hiệu dụng trên tụ cực đại, chuẩn hóa
Z L = 1 Z C = n R = 2 n − 2 ⇒ U C m a x = U 1 − n − 2 ⇒ n = 5 3
Hệ số công suất của đoạn mạch chứa RL: cos φ R L = 2 n − 2 2 n − 1 = 2 7
Đáp án A

Hệ số công suất của đoạn mạch khi xảy ra cực đại với điện áp trên tụ hoạc trên cuộn dây cos φ = 2 1 + n
Mặc khác U U L m a x 2 + 1 n 2 = 1 → ω L ω C = 2 3
→ Vậy cos φ = 2 1 + n = 0 , 96
Đáp án D

Hệ số công suất của đoạn mạch khi xảy ra cực đại với điện áp trên tụ hoạc trên cuộn dây cos φ = 2 1 + ω L ω C
Mặc khác U U L m a x 2 + ω C ω L 2 = 1 ⇒ ω C ω L = 3 2
→ Vậy cos φ = 2 1 + ω L ω C = 0 , 96
Đáp án D
Bạn áp dụng kết quả này của mạch RLC khi $w$ thay đổi để $U_C$max nhé:
\(\tan\varphi_{RL}.\tan\varphi_{mạch}=0,5\)
\(\tan\varphi_{RL}=\frac{Z_L}{R}=\frac{U_L}{U_R}=0,1\)
\(\Rightarrow\tan\varphi_{mạch}=5\)
\(\Rightarrow\cos\varphi=\frac{1}{\sqrt{1+\tan^2\varphi}}=\frac{1}{\sqrt{26}}\)