Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Lấy 3 điểm A, B, C bất kì trên đường viền. Ba điểm này tạo thành tam giác ABC và tâm và bán kính đường tròn ngoại tiếp tam giác này chính là tâm và bán kính của đường viền.
- Vẽ trung trực của 2 cạnh AB, BC, chúng cắt nhau tại O. Từ tính chất đường trung trực suy ra OA = OB = OC
Do đó O chính là tâm đường tròn này. Khi đó OA hoặc OB hoặc OC chính là bán kính cần xác định.

Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A

Để xác định được bán kính ta cần xác định được tâm của đường tròn chứa chi tiết máy này. Ta xác định tâm như sau:
+ Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy.
+ Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại D. Khi đó D là tâm cần xác định.
+ Bán kính đường tròn cần tìm là độ dài đoạn DB (hoặc DA hoặc DC).
Ta có hình vẽ minh họa
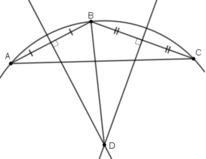

Lấy ba điểm A, B, C phân biệt trên đường viền.
Dựng đường trung trực của AB và BC. Hai đường trung trực này cắt nhau tại O.
Khi đó; OA = OB = OC
Suy ra: O là tâm của đường viền.

Hướng dẫn:

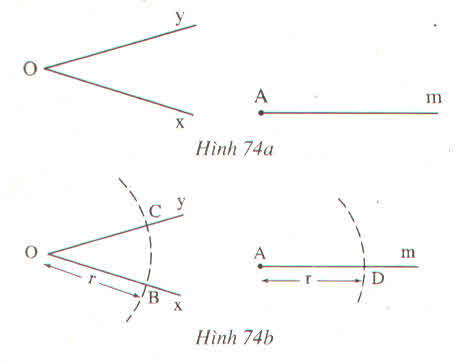
+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34

+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34

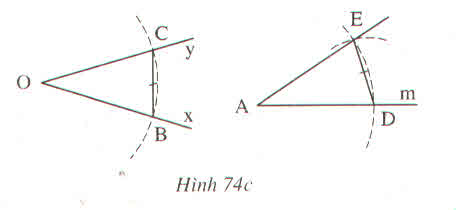
Tam giác DAE và BOC có:
AD=OB(gt)
DE=BC(gt)
AE=OC(gt)
Nên ∆ DAE= ∆ BOC(c.c.c)
suy ra \(\widehat{DAE}\)=\(\widehat{BOC}\)(hai góc tương tứng)
vậy
\(\widehat{DAE}\)=\(\widehat{xOy}\).

Hướng dẫn:
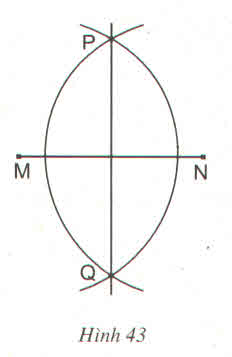
Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN
Hướng dẫn:

Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN

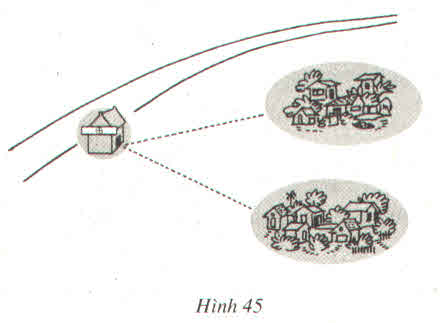
Gọi A và B là hai điểm dân cư, C là điểm đặt trạm y tế.

Vì C cách đều AB nên C thuộc đường trung trực của AB mà C ∈ xy nên C là giao điểm của xy và đường trung trực của AB
gọi 2 điểm dân cư đó là A và B, trạm y tế là C.
để C cách đểu A và B thì C phải thuộc đường trung trực của AB.
khi đó để được điểm C nằm trên đường quốc lộ và cách đều 2 điểm A,B thì C phải trùng với giao điểm của đường trung trực của AB và đường quốc lộ.
vậy trạm y tế được đặt ở giao điểm của đường quốc lộ và đường trung trực của AB.
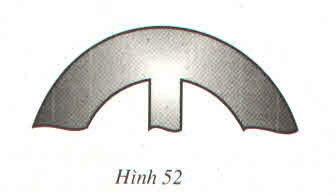
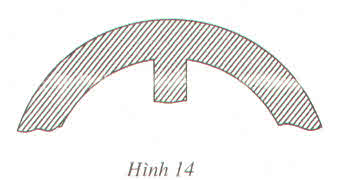

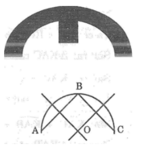
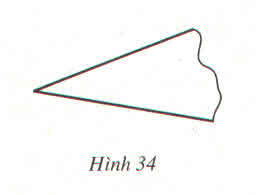
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
Hướng dẫn:
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A