K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 6 2021
\(abc\le\left(\frac{a+b+c}{3}\right)^3\Leftrightarrow\sqrt[3]{abc}\le\frac{a+b+c}{3}\)
BĐT Cô- si
5 tháng 1 2016
Thì bạn cứ biết là áp dụng bđt
\(\frac{a^2}{x}+\frac{b^2}{y}\ge\frac{\left(a+b\right)^2}{x+y}\)
5 tháng 1 2016
\(\frac{1}{a}+\frac{2}{b}=\frac{1}{a}+\frac{4}{2b}\ge\frac{\left(1+2\right)^2}{a+2b}=\frac{9}{a+2b}\) ( BĐT Schwarz )
Ta cần cm \(a+2b\le3c\)
\(\left(a+2b\right)^2=\left(1\cdot a+\sqrt{2}\cdot b\cdot\sqrt{2}\right)^2\le\left(1^2+\left(\sqrt{2}\right)^2\right)\left(a^2+2b^2\right)=3\left(a^2+2b^2\right)\le3.3c^2=9c^2\)( BUN nhiacopxki )
<=> \(\sqrt{\left(a+2b\right)^2}\le\sqrt{9c^2}\Leftrightarrow a+2b\le3c\) ( XONG )
Dấu '' = '' xảy ra khi a = b = c
7 tháng 6 2018
1/ Đặt \(\hept{\begin{cases}\sqrt{x-2013}=a\\\sqrt{x-2014}=b\end{cases}}\)
Thì ta có:
\(\frac{\sqrt{x-2013}}{x+2}+\frac{\sqrt{x-2014}}{x}=\frac{a}{a^2+2015}+\frac{b}{b^2+2014}\)
\(\le\frac{a}{2a\sqrt{2015}}+\frac{b}{2b\sqrt{2014}}=\frac{1}{2\sqrt{2015}}+\frac{1}{2\sqrt{2014}}\)
7 tháng 6 2018
2/ \(\frac{x}{2x+y+z}+\frac{y}{x+2y+z}+\frac{z}{x+y+2z}\)
\(\le\frac{1}{4}\left(\frac{x}{x+y}+\frac{x}{x+z}+\frac{y}{y+x}+\frac{y}{y+z}+\frac{z}{z+x}+\frac{z}{z+y}\right)\)
\(=\frac{3}{4}\)
5 tháng 7 2021
\(\dfrac{\sqrt{a-4}}{a}+\dfrac{\sqrt{b-4}}{b}+\dfrac{\sqrt{c-4}}{c}=\dfrac{3}{4}\) (ĐK: \(a\ge4;b\ge4;c\ge4\))
Áp dụng AM-GM có:
\(2\sqrt{4\left(a-4\right)}\le4+a-4=a\)
\(\Rightarrow\dfrac{\sqrt{a-4}}{a}\le\dfrac{1}{4}\)
Tương tự cũng có: \(\dfrac{\sqrt{b-4}}{b}\le\dfrac{1}{4}\);\(\dfrac{\sqrt{c-4}}{c}\le\dfrac{1}{4}\)
Cộng vế với vế \(\Rightarrow VT\le\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}4=a-4\\4=b-4\\4=c-4\end{matrix}\right.\)\(\Rightarrow a=b=c=8\) (tm)
Vậy...
KL
21 tháng 7 2016
Áp dụng BĐT Cô - si cho hai số không âm ta được
\(x^2+3+\frac{1}{x^2+3}\ge2\sqrt{\left(x^2+3\right)\cdot\frac{1}{x^2+3}}=2\sqrt{1}=2\)
Dấu = xảy ra \(\Leftrightarrow x^2+3=\frac{1}{x^2+3}\)
\(\Leftrightarrow\left(x^2+3\right)^2=1\)
\(\Leftrightarrow x^4+6x^2+9=1\)
\(\Leftrightarrow x^4+6x^2+8=0\)
\(\Leftrightarrow\left(x^2+2\right)\left(x^2+4\right)=0\)
\(\Leftrightarrow\left(x^2+2\right)=0\) hoặc \(\left(x^2+4\right)=0\)
\(\Leftrightarrow x^2=-2\) hoặc \(x^2=-4\) (vô nghiệm) (Sai đề r hay s á b, mik nghĩ là \(x^2-3\)ms đúng)
Vậy GTNN của M là 2
21 tháng 7 2017
Ta có bất đẳng thức Cauchy với 2 số a,b không âm :\(\frac{a+b}{2}\ge\sqrt{ab}\)
a)Gọi độ dài 2 cạnh liên tiếp của hình chữ nhật là a,b->a+b=k không đổi
->Shcn=ab\(\le\frac{\left(a+b\right)^2}{4}\)=\(\frac{k^2}{4}\)
Dấu "=" xảy ra <=>a=b<=> hình vuông
b)Gọi độ dài 2 cạnh liên tiếp của hình chữ nhật là a,b->ab=k không đổi
Chu Vi HCN=2(a+b)\(\ge\)\(4\sqrt{ab}\)=4\(\sqrt{k}\)
Dấu "=" xảy ra <=> a=b <=>Hình vuông
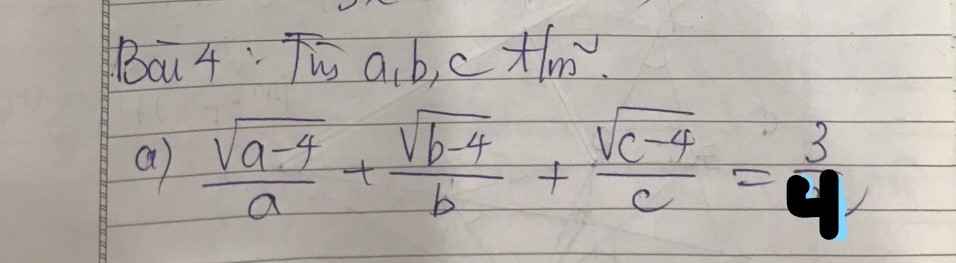
Có lẽ không đâu bn
Mà thi vào lớp 10 thì cô si với bunhiacopski là nhiều thôi bn
Thi tốt nha bn
BĐT SVAC là BĐT gif vậy cho vd mk với