Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
TH1: Chọn 2 bạn lớp A, 1 bạn B, 1 bạn C, có:
$C^2_4.C^1_5.C^1_6=180$ cách chọn
TH2: Chọn 1 bạn A, 2 bạn B, 1 bạn C, có:
$C^1_4.C^2_5.C^1_6=240$ cách chọn
TH3: Chọn 1 bạn A, 1 bạn B, 1 bạn C, có:
$C^1_4.C^1_5.C^2_6=300$ cách chọn
Tổng số cách chọn: $720$ cách chọn.
.
.
.
.
Đáp án D.
+ Số cách chọn 8 bạn bất kì : 
+ 8 bạn giỏi toán có 
cách chọn.
8 bạn giỏi hóa có 
cách chọn.
8 bạn giỏi cả toán và lý có 
cách chọn.
8 bạn giỏi cả toán và hóa có
cách chọn.
8 bạn giỏi cả lý và hóa có 
cách chọn.
8 bạn giỏi cả toán, lý, hóa là:
Đáp án A
Có 2 trường hợp như sau
+)TH1: có 3 nam, 2 nữ, suy ra có C 5 3 C 7 2 = 210 cách chọn
+) TH2: có 4 nam, 1 nữ, suy ra có C 5 4 C 7 1 = 35 cách chọn
Suy ra xác suất cần tính bằng
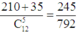
Đáp án D.
Gọi A:”Bạn được chọn có số thứ tự lớn hơn số thứ tự của Nam”.
Chọn B.
Không gian mẫu có số phần tử là 
.
Gọi A là biến cố: “Trong 5 bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ”. Khi đó, số kết quả thuận lợi cho biến cố A là: 
.
Vậy xác suất cần tính là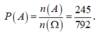 
.
Đáp án B.
- Nếu Tiến hoặc Tú làm lớp trưởng thì chỉ có 1 cách chọn lớp phó và 2 cách chọn bí thư (Tùng, Tuấn)
→ có 2.1.2 = 4 cách chọn.
- Nếu Tuấn làm lớp trưởng, thì có 2 cách chọn lớp phó (Tiến, Tú); với mỗi cách chọn lớp phó có 2 cách chọn bí thư
→ có 2.2 = 4 cách chọn.
- Số cách chọn 3 bạn cán bộ lớp là 
- Xác suất cần tìm là 
Không gian mẫu: \(C_{22}^{11}\)
Số cách chọn 11 bạn chỉ có nam hoặc nữ: \(C_{13}^{11}\)
Xác suất: \(P=\dfrac{C_{22}^{11}-C_{13}^{11}}{C_{22}^{11}}=...\)
Gọi A: “Học sinh thích môn Bóng đá”
B: “Học sinh thích môn Bóng bàn”
Do đó ta có \(P\left( A \right) = \frac{{19}}{{30}},P\left( B \right) = \frac{{17}}{{30}},P\left( {AB} \right) = \frac{{15}}{{30}}\)
Theo công thức cộng xác suất
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{19}}{{30}} + \frac{{17}}{{30}} - \frac{{15}}{{30}} = \frac{{21}}{{30}} = \frac{7}{{10}}\)
Vậy xác suất để chọn được học sinh thích ít nhất một trong hai môn Bóng đá hoặc Bóng bàn là \(\frac{7}{{10}}\)
Không gian mẫu: \(C_{25}^9\)
Chọn 9 bạn cùng 1 lớp: \(C_{10}^9\) cách
Chọn 9 bạn trong 2 lớp: \(C_{15}^9+C_{17}^9+C_{18}^9\)
Xác suất: \(P=1-\dfrac{C_{10}^9+C_{15}^9+C_{17}^9+C_{18}^9}{C_{25}^9}=...\)