K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
17 tháng 2 2017
+ sin 2x (x + kπ) = sin (2x + k2π) = sin 2x, (k ∈ Z)
(Do hàm số y = sin x có chu kì 2π).
⇒ Hàm số y = sin 2x tuần hoàn với chu kì π.
+ Hàm số y = sin 2x là hàm số tuần hoàn với chu kì π và là hàm số lẻ.
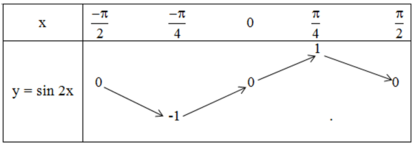
Bảng biến thiên hàm số y = sin 2x trên [-π/2; π/2]
Đồ thị:
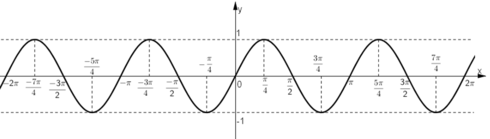
Đồ thị hàm số y = sin 2x.

17 tháng 5 2017
a) Đồ thị của hàm số \(y=\sin2x+1\) thu được từ đồ thị hàm số \(y=\sin2x\) bằng cách tịnh tiến song song với trục tung lên phía trên một đơn vị
b) Đồ thị hàm số \(y=\cos\left(x-\dfrac{\pi}{6}\right)\) thu được từ đồ thị hàm số \(y=\cos x\) bằng cách tịnh tiến song song với trục hoành sang phải một đoạn bằng \(\dfrac{\pi}{6}\)


Bài 4. Do sin (t + k2π) = sint, ∀k ∈ Z (tính tuần hoàn của hàm số f(t) = sint), từ đó sin(2π + k2π) = sin2x => sin2(tx+ kπ) = sin2x, ∀k ∈ Z.
Do tính chất trên, để vẽ đồ thị của hàm số y = sin2x, chỉ cần vẽ đồ thị của hàm số này trên một đoạn có độ dài π (đoạn.png) Chẳng hạn), rồi lại tịnh tiến dọc theo trục hoành sang bên phải và bên trái từng đoạn có độ dài π .
Chẳng hạn), rồi lại tịnh tiến dọc theo trục hoành sang bên phải và bên trái từng đoạn có độ dài π .
Với mỗi x0 ∈.png) thì x = 2x0 ∈ [-π ; π], điểm M(x ; y = sinx) thuộc đoạn đồ thị (C) của hàm số y = sinx, (x ∈ [-π ; π]) và điểm M’(x0 ; y0 = sin2x0) thuộc đoạn đồ thị (C’) của hàm số y = sin2x, ( x ∈
thì x = 2x0 ∈ [-π ; π], điểm M(x ; y = sinx) thuộc đoạn đồ thị (C) của hàm số y = sinx, (x ∈ [-π ; π]) và điểm M’(x0 ; y0 = sin2x0) thuộc đoạn đồ thị (C’) của hàm số y = sin2x, ( x ∈ .png) ) (h.5). Chú ý rằng, x = 2x0 => sinx = sin2x0 do đó hai điểm M’ , M có tung độ bằng nhau nhưng hoành độ của M’ bằng một nửa hoành độ của M. Từ đó ta thấy có thể suy ra (C’) từ (C) bằng cách “co” (C) dọc theo trục hoành như sau : với mỗi M(x ; y) ∈ (C) , gọi H là hình chiếu vuông góc của M xuống trục Oy và M’ là trung điểm của đoạn HM thì M’
) (h.5). Chú ý rằng, x = 2x0 => sinx = sin2x0 do đó hai điểm M’ , M có tung độ bằng nhau nhưng hoành độ của M’ bằng một nửa hoành độ của M. Từ đó ta thấy có thể suy ra (C’) từ (C) bằng cách “co” (C) dọc theo trục hoành như sau : với mỗi M(x ; y) ∈ (C) , gọi H là hình chiếu vuông góc của M xuống trục Oy và M’ là trung điểm của đoạn HM thì M’ .png) ∈ (C’) (khi m vạch trên (C) thì M’ vạch trên (C’)). Trong thực hành, ta chỉ cần nối các điểm đặc biệt của (C’) (các điểm M’ ứng với các điểm M của (C) với hoành độ ∈ {
∈ (C’) (khi m vạch trên (C) thì M’ vạch trên (C’)). Trong thực hành, ta chỉ cần nối các điểm đặc biệt của (C’) (các điểm M’ ứng với các điểm M của (C) với hoành độ ∈ {.png) }).
}).