Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì V ( R ) = 4 π r 3 / 3 nên V ′ ( R ) = 4 π R 2 là diện tích mặt cầu.

Vì V = π r 2 h nên V ′ ( h ) = π r 2 là diện tích đáy hình trụ;
V′(r) = 2πrh là diện tích xung quanh của hình trụ.

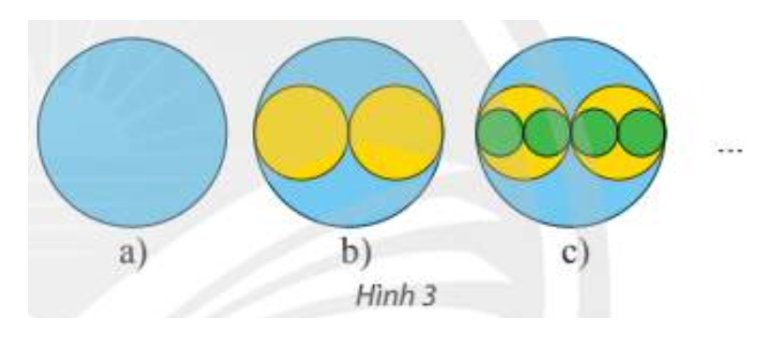
Giả sử các hình tròn bán kính \({R_1} = R,{R_2} = \frac{R}{2},{R_3} = \frac{R}{4} = \frac{R}{{{2^2}}},...,{R_n} = \frac{R}{{{2^{n - 1}}}},...\) có diện tích lần lượt là \({u_1},{u_2},{u_3},...,{u_n},...\) Ta có:
\(\begin{array}{l}{u_1} = \pi R_1^2 = \pi {R^2},{u_2} = \pi R_2^2 = \pi {\left( {\frac{R}{2}} \right)^2} = \pi {R^2}.\frac{1}{{{2^2}}},{u_3} = \pi R_3^2 = \pi {\left( {\frac{R}{{{2^2}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^4}}},...,\\{u_n} = \pi R_n^2 = \pi {\left( {\frac{R}{{{2^{n - 1}}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^{2n - 2}}}},...\end{array}\)
\(\begin{array}{l}S = {u_1} + {u_2} + ... + {u_n} + ... = \pi {R^2} + 2\pi {R^2}.\frac{1}{{{2^2}}} + 4.\pi {R^2}.\frac{1}{{{2^4}}} + ... + {2^{n + 1}}\pi {R^2}.\frac{1}{{{2^{2n - 2}}}} + ...\\\,\,\,\, = \pi {R^2} + \pi {R^2}.\frac{1}{2} + \pi {R^2}.\frac{1}{{{2^2}}} + ... + \pi {R^2}.\frac{1}{{{2^{n - 1}}}} + ...\\\,\,\,\, = \pi {R^2}\left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...} \right)\end{array}\)
Xét tổng: \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...\)
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\) và công bội \(q = \frac{1}{2}\) nên: \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ... = \frac{1}{{1 - \frac{1}{2}}} = 2\).
Vậy \(S = \pi {R^2}.{S_n} = 2\pi {R^2}\).

Gọi I' là ảnh của I qua phép biến hình nói trên
a) Phương trình của đường tròn (I;3) là ( +
= 9
b) (I) = I' (1;-1), phương trình đường tròn ảnh :
c) (I) = I'(3;2), phương trình đường tròn ảnh:
d) (I) = I'( -3;2), phương trình đường tròn ảnh:
Gọi I' là ảnh của I qua phép biến hình nói trên
a) Phương trình của đường tròn (I;3) là ( +
= 9
b) (I) = I' (1;-1), phương trình đường tròn ảnh :
c) (I) = I'(3;2), phương trình đường tròn ảnh:
d) (I) = I'( -3;2), phương trình đường tròn ảnh:

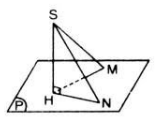
a) Giả sử ta có hai đường xiên SA, SB và các hình chiếu HA, HB của chúng trên mp(α)
Giả sử HA = HB
Vì SH ⊥ mp(α) nên SH ⊥ HA và SH ⊥ SB và các tam giác SHA, SHB là các tam giác vuông. Hai tam giác vuông SHA, SHB có canh SH chung và HA = HB nên :
ΔSHA = ΔSHB SA = SB
Ngược lại nếu SA = SB thì ΔSHA = ΔSHB ⇒ HA = HB
Kết quả, ta có HA = HB SA= SB (đpcm)
b) Giả sử có hai đường xiên SA, SC và các hình chiếu HA, HC của chúng trên mp(α) với giả thiết HC > HA.
Trên đoạn HC, lấy điểm B' sao cho HA' = HA ⇒ HC > HA'. Như vậy, theo kết quả câu a) ta có SA' = SA. Ta có trong các tam giác vuông SHB', SHC thì :
SC2= SH2 + HC2
SA2 = SH2 + HA2
Vì HC > HA' nên SC2 > SA2 ⇒ SC > SA
Suy ra SC > SA
Như vậy HC > HA ⇒ SC > SA
Lí luận tương tự, ta có : SC > SA ⇒ HC > HA
Kết quả : HC > HA ⇔ SC > SA
a) Gọi SN là một đường xiên khác. Xét hai tam giác vuông SHM và SHN có SH chung. Nếu SM = SN => tam giác SHM = tam giác SHN => HM = HN, ngược lại nếu HM = HN thì tam giác SHM = tam giác SHNSM => SM = SN.
b) Xét tam giác vuông SHM và SHN có SH chung. Nếu SN > SM thì \(HN^2-SN^2-SH^2\) => \(SM^2-SH^2=HM^2\) => HN > HM. Chứng minh tương tự cho chiều ngược lại.
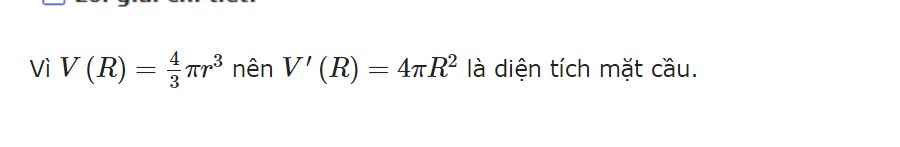

Tham khảo: