Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hỏi nhiều quá , mà thà bạn nói ko cần vẽ hình thì còn giải , đằng này đã vẽ hình còn phải ghi GT , KL . mệt !!!!!!!!!!! @_@
Chứng Minh Định lý hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì chúng song song với nhau

d:
Giả thiết: \(\widehat{xAy}\) và \(\widehat{x'Ay'}\) là hai góc đối đỉnh
Kết luận: \(\widehat{xAy}=\widehat{x'Ay'}\)

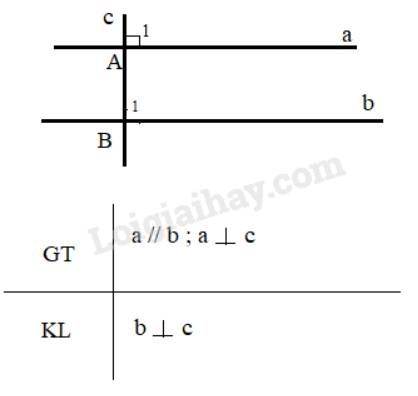
Giả sử cho 2 đường thẳng song song a và b, đường thẳng c vuông góc với a. Ta phải chứng minh c cũng vuông góc với b. Thật vậy:
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) ( 2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \) nên \(\widehat {{B_1}} = 90^\circ \) hay \(b \bot c\)
Vậy một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.
Trong chứng minh trên, ta đã sử dụng tính chất của hai đường thẳng song song.

Bài 1:
| GT | a\(\perp\)b;b\(\perp\)c |
| KL | a//c |
Ta có: a\(\perp\)b
b\(\perp\)c
Do đó: a//c(Định lí 1 từ vuông góc tới song song)
Bài 2:
| GT | a\(\perp\)b;b//c |
| KL | a\(\perp\)c |
Ta có: b//c
a\(\perp\)b
Do đó: a\(\perp\)c

1. Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.
2.Qua một điểm nằm ngoài một đường thẳng ta vẽ được một và chỉ một đường thẳng song song với đường thẳng đã cho.
3.Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
4.Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì ba đường thẳng đều song song.5.Đường thẳng vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng còn lại.