Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đặt vế trái bằng \(S_n\).
Với n = 1. Vế trái chỉ có một số hạng bằng 2, vế phải bằng \(\dfrac{1.\left(3.1+1\right)}{2}=2\).
Vậy \(VP=VT\). Điều cần chứng minh đúng với n = 1.
Giả sử có \(S_k=\dfrac{k\left(3k+1\right)}{2}\). Ta phải chứng minh:
\(S_{k+1}=\dfrac{\left(k+1\right)\left[3\left(k+1\right)+1\right]}{2}=\dfrac{\left(k+1\right)\left(3k+4\right)}{2}\).
Thật vậy ta có:
\(S_{k+1}=S_k+\left[3\left(k+1\right)-1\right]\)\(=\dfrac{k\left(3k+1\right)}{2}+\left[3\left(k+1\right)-1\right]\)
\(=\dfrac{k\left(3k+1\right)}{2}+\dfrac{2\left(3k+2\right)}{2}\)\(=\dfrac{3k^2+7k+4}{2}=\dfrac{\left(k+1\right)\left(3k+4\right)}{ }\).
Vậy \(S_n=\dfrac{n\left(3n+1\right)}{2}\).
b) Đặt vế trái bằng \(S_n\).
Với n = 1.
VT = 3; VP \(=\dfrac{1}{2}\left(3^2-3\right)=3\).
Điều cần chứng minh đúng với n = 1.
Giả sử \(S_k=\dfrac{1}{2}\left(3^{k+1}-3\right)\).
Ta cần chứng minh: \(S_{k+1}=\dfrac{1}{2}\left(3^{k+1+1}-3\right)=\dfrac{1}{2}\left(3^{k+2}-3\right)\).
Thật vậy:
\(S_{k+1}=S_k+3^{k+1}=\dfrac{1}{2}\left(3^{k+1}-3\right)+3^{k+1}\)
\(=\dfrac{1}{2}\left(3^{k+1}-3+2.3^{k+1}\right)=\dfrac{1}{2}\left(3.3^{k+1}-3\right)\)\(=\dfrac{1}{2}\left(3^{k+2}-3\right)\).
Vậy \(S_n=\dfrac{1}{2}\left(3^{n+1}-3\right)\).
a) Với n = 1, vế trái chỉ có một số hạng là 2, vế phải bằng = 2
Vậy hệ thức đúng với n = 1.
Đặt vế trái bằng Sn.
Giả sử đẳng thức a) đúng với n = k ≥ 1, tức là
Sk= 2 + 5 + 8 + …+ 3k – 1 =
Ta phải chứng minh rằng cũng đúng với n = k + 1, nghĩa là phải chứng minh
Sk+1 = 2 + 5 + 8 + ….+ 3k -1 + (3(k + 1) – 1) =
Thật vậy, từ giả thiết quy nạp, ta có: Sk+1 = Sk + 3k + 2 = + 3k + 2
=
(điều phải chứng minh)
Vậy theo nguyên lí quy nạp toán học, hệ thức đúng với mọi n ε N*
b) Với n = 1, vế trái bằng , vế phải bằng
, do đó hệ thức đúng.
Đặt vế trái bằng Sn.
Giả sử hệ thức đúng với n = k ≥ 1, tức là
Ta phải chứng minh .
Thật vậy, từ giả thiết quy nạp, ta có:
= (điều phải chứng minh)
Vậy theo nguyên lí quy nạp toán học, hệ thức b) đúng với mọi n ε N*
c) Với n = 1, vế trái bằng 1, vế phải bằng = 1 nên hệ thức đúng với n = 1.
Đặt vế trái bằng Sn.
Giả sử hệ thức c) đúng với n = k ≥ 1, tức là
Sk = 12 + 22 + 32 + …+ k2 =
Ta phải chứng minh
Thật vậy, từ giả thiết quy nạp ta có:
Sk+1 = Sk + (k + 1)2 = = (k + 1).
= (k + 1)
(đpcm)
Vậy theo nguyên lí quy nạp toán học, hệ thức đúng với mọi n ε N*
\(=lim\frac{1}{2\sqrt{2}n\sqrt[4]{1+\frac{3}{64n}-\frac{1}{32n^2}+\frac{1}{64n^4}}-n\sqrt{1-\frac{3}{n}+\frac{5}{n^2}}-3n}\)
\(=lim\frac{1}{2\sqrt{2}n-n-3n}=lim\frac{1}{\left(2\sqrt{2}-4\right)n}=0\)
\(a=lim\frac{n^2+n}{6n^3}=lim\frac{\frac{1}{n}+\frac{1}{n^3}}{6}=\frac{0}{6}=0\)
\(b=lim\frac{1+\frac{2}{n}}{1+\frac{1}{n}}+lim\frac{sinn}{2^n}=1+0=1\)
Giải thích: \(-1\le sin\left(n\right)\le1\) \(\forall n\Rightarrow\frac{-1}{2^n}\le\frac{sin\left(n\right)}{2^n}\le\frac{1}{2^n}\)
Mà \(lim\frac{-1}{2^n}=lim\frac{1}{2^n}=0\Rightarrow lim\frac{sin\left(n\right)}{2^n}=0\) theo nguyên tắc giới hạn kẹp
\(c=lim\frac{-3n-1}{\sqrt{n^2-3n}+\sqrt{n^2+1}}=lim\frac{-3-\frac{1}{n}}{\sqrt{1-\frac{3}{n}}+\sqrt{1+\frac{1}{n^2}}}=\frac{-3}{1+1}=-\frac{3}{2}\)
\(d=lim\frac{3n^2}{\sqrt[3]{\left(n^3+3n^2\right)^2}+n\sqrt[3]{n^3+3n^2}+n^2}=lim\frac{3}{\sqrt[3]{\left(1+\frac{3}{n}\right)^2}+\sqrt[3]{1+\frac{3}{n}}+1}=\frac{3}{1+1+1}=1\)
Đặt vế trái bằng S n . Kiểm tra với n = 1 hệ thức đúng.
Giả sử đã có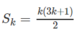 
với k ≥ 1.
Ta phải chứng minh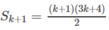 
Thật vậy
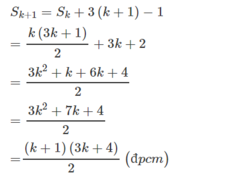
\(=lim\frac{3+\frac{2}{n}+\frac{5}{n^2}}{7+\frac{1}{n}-\frac{8}{n^2}}=\frac{3}{7}\)
\(=lim-3n^3\left(1-\frac{5}{3n^2}+\frac{2}{3n^3}\right)=-\infty\)
\(=lim\frac{\left(\frac{3}{7}\right)^n+4}{3-2.\left(\frac{1}{7}\right)^n}=\frac{4}{3}\)
Câu này đề thiếu, giới hạn của x nên nó là giới hạn của hàm chứ ko phải giới hạn của dãy, mà giới hạn của hàm thì cần chỉ rõ x tiến tới bao nhiêu mới tính được
\(=lim\frac{\left(\frac{1}{3}\right)^n-1}{\left(\frac{2}{3}\right)^n+4}=-\frac{1}{4}\)
\(A=lim\frac{\sqrt{n+2}+\sqrt{n+1}}{1}=lim\left[n\left(\sqrt{1+\frac{2}{n}}+\sqrt{1+\frac{1}{n}}\right)\right]=+\infty.2=+\infty\)
\(B=lim\frac{8^3.64^n-9.27^n}{4^4.64^n+5^3.25^n}=\frac{8^3-9.\left(\frac{27}{64}\right)^n}{4^4+5^3\left(\frac{25}{64}\right)^n}=\frac{8^3}{4^4}=2\)
\(1;-\frac{1}{2};\frac{1}{4}...\) là dãy cấp số nhân lùi vô hạn có \(u_1=1\) và \(q=-\frac{1}{2}\)
Do \(\left|q\right|< 1\) nên theo công thức tổng cấp số nhân:
\(S_n=\frac{u_1}{1-q}=\frac{1}{1+\frac{1}{2}}=\frac{2}{3}\)
tham khảo:
\(a) 2+5+8+...+(3n−1)=n(3n+1)2 (1) Đặt Sn=2+5+8+...+(3n−1) Với n=1 ta có: S1=2=1(3.1+1)2 Giả sử (1) đúng với n=k(k≥1), tức là Sk=2+5+8+...+(3k−1)=k(3k+1)2 Ta chứng minh (1) đúng với n=k+1 hay Sk+1=(k+1)(3k+4)2 Thật vậy ta có: Sk+1=2+5+8+...+(3k−1)+[3(k+1)−1]=Sk+3k+2=k(3k+1)2+3k+2=3k2+k+6k+42=3k2+7k+42=(k+1)(3k+4)2 Vậy (1) đúng với mọi k≥1 hay (1) đúng với mọi n∈N∗ b) 3+9+27+...+3n=12(3n+1−3) (2) Đặt Sn=3+9+27+...+3n=12(3n+1−3) Với n=1, ta có: S1=3=12(32−3) (hệ thức đúng) Giả sử (2) đúng với n=k(k≥1) tức là Sk=3+9+27+...+3k=12(3k+1−3) Ta chứng minh (2) đúng với n=k+1, tức là chứng minh Sk+1=12(3k+2−3) Thật vậy, ta có: Sk+1=3+9+27+...+3k+1=Sk+3k+1=12(3k+1−3)+3k+1=32.3k+1−32=12(3k+2−3)(đpcm) Vậy (2) đúng với mọi k≥1 hay đúng với mọi n∈N∗\)