NH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
16 tháng 9 2023
Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
$A\geq \frac{9}{x+2+y+2+z+2}=\frac{9}{x+y+z+6}$
Áp dụng BĐT Bunhiacopxky:
$(x^2+y^2+z^2)(1+1+1)\geq (x+y+z)^2$
$\Rightarrow 9\geq (x+y+z)^2\Rightarrow x+y+z\leq 3$
$\Rightarrow A\geq \frac{9}{x+y+z+6}\geq \frac{9}{3+6}=1$
Vậy $A_{\min}=1$. Dấu "=" xảy ra khi $x=y=z=1$
TN
27 tháng 5 2018
\(VT=6\left(x^2+y^2+z^2\right)+10\left(xy+yz+xz\right)+2\left(\frac{1}{2x+y+z}+\frac{1}{x+2y+z}+\frac{1}{x+y+2z}\right)\)
\(=6\left(x+y+z\right)^2-2\left(xy+yz+xz\right)+2\frac{9}{2x+y+z+x+2y+z+x+y+2z}\)
\(\ge6\left(x+y+z\right)^2-2\frac{\left(x+y+z\right)^2}{3}+2\frac{9}{4\left(x+y+z\right)}\)
\(=\: 6\cdot\left(\frac{3}{4}\right)^2-2\cdot\frac{\left(\frac{3}{4}\right)^2}{3}+2\cdot\frac{9}{4\cdot\frac{3}{4}}=9\)
CM
12 tháng 10 2017
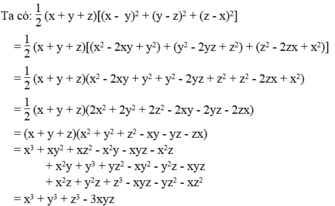
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu x ≥ 0, y ≥ 0, z ≥ 0 thì:
x + y + z ≥ 0
x - y 2 + y - z 2 + z - x 2 ≥ 0
Suy ra:
x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z
Hay: x 3 + y 3 + z 3 3 ≥ x y z
HP
cho x,y,z>0 và x+y+z=4. CMR \(\frac{1}{x^2+4yz}+\frac{1}{y^2+4xz}+\frac{1}{z^2+4xy}< \frac{1}{xyz}\)
0
NP
0
TL
1
KN
6 tháng 12 2019
Áp dụng BĐT Cô - si cho 3 số không âm:
\(x+y+z\ge3\sqrt[3]{xyz}\)hay \(1\ge3\sqrt[3]{xyz}\)
\(\Rightarrow\sqrt[3]{xyz}\le\frac{1}{3}\Rightarrow xyz\le\frac{1}{27}\)
(Dấu "="\(\Leftrightarrow x=y=z=\frac{1}{3}\))
Lại áp dụng BĐT Cô - si cho 3 số không âm là x + y; y + z; x + z, ta được:
\(\left(x+y\right)+\left(y+z\right)+\left(z+x\right)\ge3\sqrt[3]{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\)
\(\Rightarrow2\ge3\sqrt[3]{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\)(Vì x + y + z = 1)
\(\Rightarrow27\left(x+y\right)\left(y+z\right)\left(x+z\right)\le8\)(lập phương hai vế)
\(\Rightarrow\left(x+y\right)\left(y+z\right)\left(x+z\right)\le\frac{8}{27}\)
(Dâú "="\(\Leftrightarrow x=y=z=\frac{1}{3}\))
\(\Rightarrow S\le\frac{1}{27}.\frac{8}{27}=\frac{8}{729}\)(Dâú "="\(\Leftrightarrow x=y=z=\frac{1}{3}\))
NM
1
KN
29 tháng 11 2019
Ta có: \(\frac{1}{1+x}=2-\frac{1}{1+y}-\frac{1}{1+z}\)
\(=1-\frac{1}{1+y}+1-\frac{1}{1+z}=\frac{y}{1+y}+\frac{z}{1+z}\)
\(\ge2\sqrt{\frac{yz}{\left(1+y\right)\left(1+z\right)}}\)(BĐT Cô - si)
Tương tự, ta có: \(\frac{1}{1+y}\)\(\ge2\sqrt{\frac{xz}{\left(1+x\right)\left(1+z\right)}}\); \(\frac{1}{1+z}\)\(\ge2\sqrt{\frac{xy}{\left(1+x\right)\left(1+y\right)}}\)
Nhân từng vế của các bđt trên, ta được:
\(\frac{1}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\ge8.\frac{xyz}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\)
\(\Rightarrow8xyz\le1\Rightarrow xyz\le\frac{1}{8}\)
(Dấu "="\(\Leftrightarrow x=y=z=\frac{1}{2}\))