
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


X3 + Y3 = X3 + 3X2Y + 3 XY2+ Y2+ 3XY - 3 X2Y- 3XY2
=(x + y )3 + 3xy. ( 1 - x - y )
=( x + y)3 + 3xy . [ 1 - (x - y) ]
= 13 + 3xy. ( 1-1)
=1
mik cũng ko chắc nữa nhé
Ta có :x3 +y3 +3xy=(x+y)(x2 -xy+y2)+3xy
mà x+y=1
=>x2 -xy+y2+3xy=x2 +2xy+y2 =(x+y)2=12 =1

Ta có: x2+y=y2+x
=>x2+y-y2+x=0
=>(x2-y2)-(x-y)=0
=>(x-y)(x+y)-(x-y)=0
=>(x-y)(x+y-1)=0
=>x-y=0 hoặc x+y-1=0
=>x+y=1(TH1 loại do x khác y)
ta có:A=x3+y3+3xy(x2+y2)+6x2y2(x+y)
=>A=(x+y)(x2-xy+y2)+3x3y+3xy3+6x2y2
=>A=x2-xy+y2+3x3y+3xy3+6x2y2
=>A=(x+y)2-3xy+3x2y(x+y)+3xy2(x+y)
=>A=1-3xy+3x2y+3xy2
=>A=1+3xy(-1+a+b)
=>A=1+3xy(-1+1)
=>A=1+3xy.0
=>A=1
Vậy A=1 khi x2+y=y2+x và x khác y.

x3+y3=x3+3x2y+3xy2+y2+3xy-3x2y-3xy2
=(x+y)3+3xy.(1-x-y)
=(x+y)3+3xy.[1-(x+y)]
=13+3xy.(1-1)
=1

a) Ta có hằng đẳng thức \(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
Vậy nên \(a^3+b^3+c^3+6=0.\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)
\(\Rightarrow a^3+b^3+c^3=-6.\)
b) \(x^3+y^3+3xy=x^3+3xy\left(x+y\right)+y^3=x^3+3x^2y+3xy^2+y^3=\left(x+y\right)^3=1.\)
c) \(x^3-y^3-3xy=x^3-3xy\left(x-y\right)-y^3=x^3-3x^2y+3xy^2-y^3=\left(x-y\right)^3=1.\)

1. Áp dụng bất đẳng thức \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\) với \(a=x^3+3xy^2,b=y^3+3x^2y\) (a;b > 0)
(Bất đẳng thức này a;b > 0 mới dùng được)
\(A\ge\frac{4}{x^3+3xy^2+y^3+3x^2y}=\frac{4}{\left(x+y\right)^3}\ge\frac{4}{1^3}=4\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}x^3+3xy^2=y^3+3x^2y\\x+y=1\end{cases}\Leftrightarrow\hept{\begin{cases}x^3-3x^2y+3xy^2-y^3=0\\x+y=1\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x-y\right)^3=0\\x+y=1\end{cases}}\Leftrightarrow x=y=\frac{1}{2}\)

\(P=x^3+3xy+y^3=x^3+3xy\left(x+y\right)+y^3=\left(x+y\right)^3=1^3=1\)

x2-y=y2-x
<=>(x2-y2)+(x-y)=0
<=>(x-y)(x+y)+(x-y)=0
<=>(x-y)(x+y+1)=0
*)Nếu x-y=0<=>x=y
Tính a theo x ta có
A=x3+x3+3x2(x2+x2)+6x4(x+x)
=2x3+6x4+12x5
*)Nếu x+y+1=0
<=>x=-(y+1)
Tính A theo y ta có
A=(-y-1)3+y3+3(y-1)y[(-y-1)2+y2]+6(-y-1)2y2(-y-1+y)
cái này bạn tự tính


b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
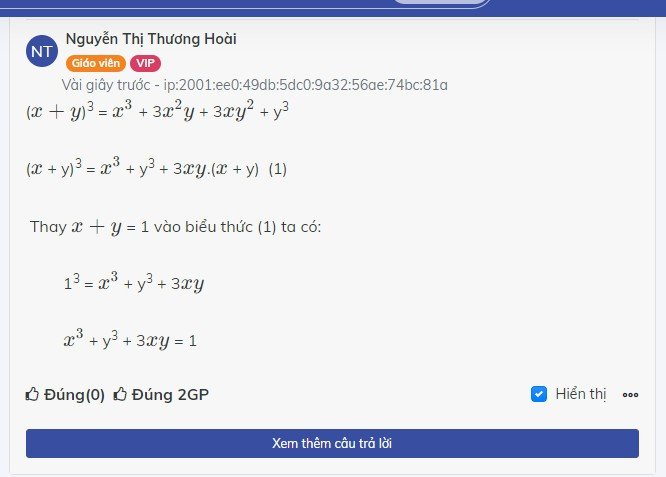
Từ x+y=1 (GT)
=>(x+y)3=13=1
=>x3+3x2y+3xy2+y3=1 (HĐT)
=>x3+y3+3xy(x+y)=1
=>x3+y3+3xy*1=1
=>x3+y3+3xy=1