
f(x) = f(a);
f(x)= f(b).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f(x) = f(a);
f(x)= f(b).

Xét hàm số
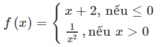
- Trường hợp x ≤ 0
f(x) = x + 2 là hàm đa thức, liên tục trên R nên nó liên tục trên (-2; 0]
- Trường hợp x > 0
f ( x ) = 1 / x 2 là hàm số phân thức hữu tỉ nên liên tục trên (2; 0) thuộc tập xác định của nó.
Như vậy f(x) liên tục trên (-2; 0] và trên (0; 2)
Tuy nhiên, vì 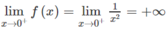 nên hàm số f(x) không cógiới hạn hữu hạn tại x = 0. Do đó, nó không liên tục tại x = 0. Nghĩa là không liên tục trên (-2; 2)
nên hàm số f(x) không cógiới hạn hữu hạn tại x = 0. Do đó, nó không liên tục tại x = 0. Nghĩa là không liên tục trên (-2; 2)

Vì hàm số liên tục trên (a; b] nên liên tục trên (a; b) và
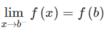 (1)
(1)
Vì hàm số liên tục trên [b; c) nên liên tục trên (b; c) và
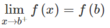 (2)
(2)
Từ (1) và (2) suy ra f(x) liên tục trên các khoảng (a; b), (b; c) và liên tục tại x = b
(vì 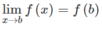 ).
).
Nghĩa là nó liên tục trên (a; c)

Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Ví dụ minh hoạ :
- f ( x ) = x 2 − 1 liên tục trên đoạn [−2;2], f(−2).f(2) = 9 > 0
Phương trình x 2 – 1 = 0 có nghiệm x = 1 hoặc x = -1 trong khoảng (-2; 2)
- f ( x ) = x 2 + 1 liên tục trên đoạn [-1; 1] và f(−1).f(1) = 4 > 0. Còn phương trình x 2 + 1 = 0 lại vô nghiệm trong khoảng (-1; 1)

+ Hàm số liên tục tại một điểm

+ Hàm số liên tục trên một khoảng
- Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
- Hàm số y = f(x) được gọi là liên tục trên một đoạn [a; b] nếu nó liên tục tại mọi điểm thuộc khoảng (a;b) và
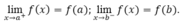
Đồ thị của hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.

1. Hàm không liên tục tại \(x=-1\) nên đáp án A sai
2. Hàm liên tục tại \(x=0,5\)
3. Đề thiếu
4. \(\lim\limits_{x\rightarrow-2^-}f\left(x\right)=3.\left(-2\right)-5=-11\)
\(\lim\limits_{x\rightarrow-2^+}f\left(x\right)=-2a-1\)
Hàm liên tục tại x=-2 khi:
\(-2a-1=-11\Rightarrow a=-5\)