Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
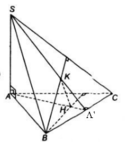
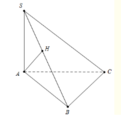
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ A là hình chiếu của A trên mặt phẳng (ABC)
\( \Rightarrow \) HA là hình chiếu của SA trên mặt phẳng (ABC)
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ B là hình chiếu của B trên mặt phẳng (ABC)
\( \Rightarrow \) HB là hình chiếu của SB trên mặt phẳng (ABC)
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ C là hình chiếu của C trên mặt phẳng (ABC)
\( \Rightarrow \) HC là hình chiếu của SC trên mặt phẳng (ABC)
b, Do H là hình chiếu của S trên mặt phẳng (ABC) \( \Rightarrow SH \bot (ABC)\).
Mà \(AB,AC,BC \subset (ABC) \Rightarrow SH \bot AB,SH \bot AC,SH \bot BC\).
Ta có: \(\left\{ \begin{array}{l}SA \bot BC\\SH \bot BC\\SA \cap SH = S\\SA,SH \subset (SAH)\end{array} \right. \Rightarrow BC \bot (SAH) \Rightarrow BC \bot AH\,(1)\)
Tương tự \(\left\{ \begin{array}{l}SC \bot AB\\SH \bot AB\\SC \cap SH = S\\SC,SH \subset (SCH)\end{array} \right. \Rightarrow AB \bot (SCH) \Rightarrow AB \bot CH\,(2)\)
TỪ (1) và (2) \( \Rightarrow \) H là trực tâm của tam giác ABC.
Vì \(\left\{ \begin{array}{l}AB \bot (SCH)\\SC \subset (SCH)\end{array} \right. \Rightarrow AB \bot SC\)

TenAnh1 TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) E = (-3.34, -5.86) E = (-3.34, -5.86) E = (-3.34, -5.86) F = (12.02, -5.86) F = (12.02, -5.86) F = (12.02, -5.86) G = (-3.7, -5.88) G = (-3.7, -5.88) G = (-3.7, -5.88) H = (11.66, -5.88) H = (11.66, -5.88) H = (11.66, -5.88) I = (-3.74, -5.62) I = (-3.74, -5.62) I = (-3.74, -5.62) J = (11.62, -5.62) J = (11.62, -5.62) J = (11.62, -5.62) A'


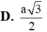


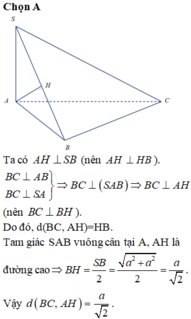
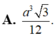
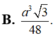
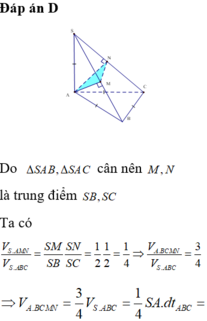
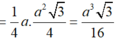

S A B C H
SH vuông góc (ABC) => AC vuông góc SH, mà AC vuông góc BH nên AC vuông góc (SHB)
=> SB vuông góc AC, kết hợp với SB vuông góc SA => SB vuông góc SC => SA,SB,SC đôi một vuông góc
Từ đó, theo định lì Pytago và BĐT \(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}\):
\(6\left(SA^2+SB^2+SC^2\right)=3\left(AB^2+BC^2+CA^2\right)\ge3.\frac{\left(AB+BC+CA\right)^2}{3}=\left(AB+BC+CA\right)^2\)
lol Vc lol