Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao:
AI ⊥ BC
+) Tương tự, tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao:
DI ⊥ BC
+) Ta có: 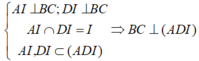
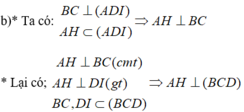

a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI ⊥ BC. Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI ⊥ BC. Ta suy ra:
BC ⊥ (AID) nên BC ⊥ AD.
b) Vì BC ⊥ (AID) nên BC ⊥ AH
Mặt khác AH ⊥ ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).

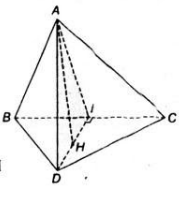
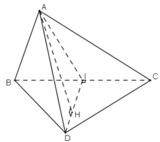
Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung đáy BC. Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
b) Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng (BCD).

a) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao:
AI ⊥ BC
+) Tương tự, tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao:
DI ⊥ BC
Mặt khác AH⊥ID nên ta suy ra AH vuông góc với mặt phẳng (BCD)
HT

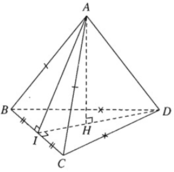
CMR: BC ⊥ (ADH) và DH = a.
● Δ ABC đều, H là trung điểm BC nên AH BC, AD BC
⇒ BC ⊥ (ADH) ⇒ BC ⊥ DH.
⇒ DH = d(D, BC) = a

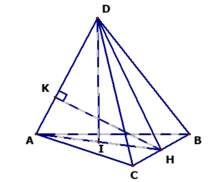
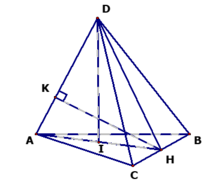
CMR: DI ⊥ (ABC).
● AD = a, DH = a ΔDAH cân tại D.
- Mặt khác I là trung điểm của AH nên DI ⊥ AH.
● BC ⊥ (ADH) ⇒ BC ⊥ DI.
⇒ DI ⊥ (ABC).

Bài 1:
I là trung điểm BC \(\Rightarrow AI\perp BC\) (trung tuyến đồng thời là đường cao)
Tương tự \(ID\perp BC\)
\(\Rightarrow BC\perp\left(AID\right)\)
b/ \(AH\perp\left(AID\right)\Rightarrow BC\perp AH\)
Mà \(AH\perp DH\)
\(\Rightarrow AH\perp\left(BCD\right)\)
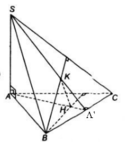
Bài 2:
\(SA=SC\Rightarrow\Delta SAC\) cân tại S \(\Rightarrow SO\perp AC\) (trung tuyến là đường cao)
Tương tự \(\Delta SBD\) cân tại S \(\Rightarrow SO\perp BD\)
\(\Rightarrow SO\perp\left(ABCD\right)\)
b/ \(SC=SD\Rightarrow\Delta SCD\) cân tại S \(\Rightarrow SI\perp CD\)
Mà \(SO\perp\left(ABCD\right)\Rightarrow SO\perp CD\)
\(\Rightarrow CD\perp\left(SOI\right)\)
c/ \(SO\perp\left(ABCD\right)\Rightarrow SO\perp BD\)
Mà \(AC\perp BD\) (2 đường chéo hv)
\(\Rightarrow BD\perp\left(SAC\right)\)
d/ \(CD\perp\left(SOI\right)\Rightarrow CD\perp IJ\)
Mà \(OJ\perp SI\)
\(\Rightarrow OJ\perp\left(SCD\right)\Rightarrow OJ\perp SD\)