Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A A A B B B C C C M M M N N N H H H K K K I I I O O O \(\Delta BMC:\widehat{BMC}=90^0;OB=OC\Rightarrow OM=OB=OC\Rightarrow\widehat{OMC}=\widehat{ACB}\left(1\right)\)(do tam giác OMC cân)
\(\Delta AMH:\widehat{AMH}=90^0;AI=HI\Rightarrow AI=HI=IM\Rightarrow\widehat{IAM}=\widehat{IMA}\left(2\right)\)(do tam giác IAM cân)
\(\left(1\right),\left(2\right)\Rightarrow\widehat{IMA}+\widehat{OMC}=\widehat{IAM}+\widehat{OCM}=90^0\Rightarrow\widehat{IMO}=90^0\)
Tương tự thì \(\widehat{INO}=90^0\)
Suy ra \(\widehat{NIM}+\widehat{NOM}=180^0\left(DPCM\right)\)

Giải thích các bước giải:
a) Ta có:
Do CH là đường cao của tam giác ABC nên CH vuông góc với AB mà theo giả thiết thì BK cũng vuông góc với AB nên suy ra CH song song với BK.
Tương tự chứng minh trên ta cũng có: BH song song với CK
Tứ giác BHCK có : BH song song CK và CH song song BK nên tứ giác BHCK là hình bình hành.
b) Theo kết quả của phần A ta có:
BHCK là hình bình hành có 2 đường chéo BC và HK ⇒ BC và HK cắt nhau tại trung điểm mỗi đường (Tính chất của hình bình hành) mà M là trung điểm BC suy ra M là trung điểm HK ⇒ H,M,K thẳng hàng.
Xét tam giác AHK có: M là trung điểm HK, I là trung điểm AK
⇒ MI là đường trung bình của tam giác AHK
⇒ MI song song với AH và MI=1/2 AH.
mik ko biết đúng hay ko nữa

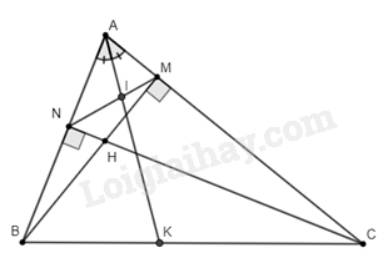
a) Vì \(BM\)là đường cao nên \(\widehat {AMB} = 90^\circ \); vì \(CN\)là đường cao nên \(\widehat {ANC} = 90^\circ \)
Xét tam giác \(AMB\) và tam giác \(ANC\) có:
\(\widehat A\) (chung)
\(\widehat {ANB} = \widehat {ANC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AMB\backsim\Delta ANC\) (g.g).
Suy ra, \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (tỉ lệ thức)
Xét tam giác \(AMN\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (chứng minh trên)
Suy ra, \(\Delta AMN\backsim\Delta ABC\) (c.g.c).
b) Xét tam giác \(AMN\) có \(AI\) là đường phân giác của \(\widehat {MAN}\left( {I \in MN} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}\)
Xét tam giác \(ABC\) có \(AK\) là đường phân giác của \(\widehat {BAC}\left( {K \in BC} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}\)
Mà \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (chứng minh trên) nên \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\) (điều phải chứng minh).