Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b: Xét tứ giác MNHQ có
K là trung điểm của MH
K là trung điểm của NQ
Do đó: MNHQ là hình bình hành
Suy ra: MQ=HN
Hướng dẫn :
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)
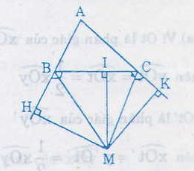
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của góc ˆBACBAC^
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của gócA
. Trên cạnh AB lấy điểm D sao cho 
, trên cạnh AC lấy điểm E sao cho 
. Gọi I là giao điểm của CD và BE. Kẻ IH ⊥ AC, IK ⊥ BC (H∈AC, K∈BC). Trên tia đối của tia HI lấy điểm M sao cho MH = HI, trên tia IK lấy điểm N sao cho K là trung điểm của IN
.
a: Xét tứ giác MNEQ có
K là trung điểm của ME
K là trung điểm của NQ
Do đó: MNEQ là hình bình hành
Suy ra: MN//EQ
b: \(\widehat{NKE}=180^0-50^0-25^0=105^0\)
c: Xét tứ giác MIEG có
MI//EG
MI=EG
Do đó: MIEG là hình bình hành
Suy ra: ME cắt GI tại trung điểm của mỗi đường
=>K là trung điểm của GI