Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,BC=\sqrt{AB^2+AC^2}=15\left(cm\right)\left(pytago\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot CH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=5,4\left(cm\right)\\CH=\dfrac{AC^2}{BC}=9,6\left(cm\right)\\AH=\sqrt{5,4\cdot9,6}=51,84\left(cm\right)\end{matrix}\right.\)
\(b,\sin B=\cos C=\dfrac{AC}{BC}=\dfrac{4}{5}\\ \cos B=\sin C=\dfrac{AB}{BC}=\dfrac{3}{5}\\ \tan B=\cot C=\dfrac{AC}{AB}=\dfrac{4}{3}\\ \cot B=\tan C=\dfrac{AB}{AC}=\dfrac{3}{4}\)

Sử dụng các tỉ số lượng giác, tính được:
sinB = 3 5 ; cosB = 4 5 ; tanB = 3 4 ; cotB = 4 3
=> sinA = 4 5 ; cosA = 3 5 ; tanA = 4 3 ; cotA = 3 4

a: Xét ΔMNE vuông tại M có
\(MN^2+ME^2=NE^2\)
hay ME=4(cm)

c) Xét tứ giác FMHN có
\(\widehat{NFM}=90^0\)
\(\widehat{FNH}=90^0\)
\(\widehat{FMH}=90^0\)
Do đó: FMHN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Hình chữ nhật FMHN có đường chéo FH là tia phân giác của \(\widehat{NFM}\)(gt)
nên FMHN là hình vuông(Dấu hiệu nhận biết hình vuông)

Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=8(cm)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
\(\cos\widehat{B}=\dfrac{3}{5}\)
\(\tan\widehat{B}=\dfrac{4}{3}\)
\(\cot\widehat{B}=\dfrac{3}{4}\)

Câu hỏi của Pham Van Hung - Toán lớp 9 - Học toán với OnlineMath
Bạn tham khảo link này nhé!

a: ΔDEF vuông tại D
=>\(DE^2+DF^2=EF^2\)
=>\(EF^2=0,9^2+12^2=144,81\)
=>\(EF=\sqrt{144,81}\)(cm)
Xét ΔDEF vuông tại D có \(tanE=\dfrac{DF}{DE}\)
=>\(tanE=\dfrac{12}{0,9}=\dfrac{120}{9}=\dfrac{40}{3}\)
b: Xét ΔDEF vuông tại D có
\(sinF=\dfrac{DE}{EF}=\dfrac{0.9}{\sqrt{144,81}}\)
\(cosF=\dfrac{DF}{EF}=\dfrac{12}{\sqrt{144,81}}\)
\(tanF=\dfrac{0.9}{12}=\dfrac{9}{120}=\dfrac{3}{40}\)
\(cotF=\dfrac{12}{0.9}=\dfrac{40}{3}\)

Theo định lý Py-ta-go ta có:
![]()
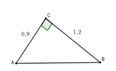
Xét tam giác ABC vuông tại C có:
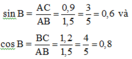
Đáp án cần chọn là: A

Ta có: ΔABC vuông tại A
mà \(AC=\dfrac{1}{2}BC\)
nên \(\widehat{B}=30^0\)
\(\sin\widehat{B}=\dfrac{1}{2}\)
\(\cos\widehat{B}=\dfrac{\sqrt{3}}{2}\)
\(\tan\widehat{B}=\dfrac{\sqrt{3}}{3}\)
\(\cot\widehat{B}=\sqrt{3}\)
GF=căn 0,9^2+1,2^2=1,5cm
sin G=cos F=EF/GF=3/5
cosG=sin F=EG/GF=4/5
tan G=cot F=3/5:4/5=3/4
cot G=tan F=4/3