Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Theo BĐT tam giác thì:
$AC< AB+AC$ hay $AC< 9$
$BC< AB+AC$ hay $7< 2+AC$ hay $AC>5$ (cm)
Vậy $9> AC> 5$. Mà $AC$ là số nguyên tố nên $AC=7$

AB là
( 49 + 7 ) : 2 = 28
AC là
28 - 7 = 21
Xét tam giác ABC vuông tại A
AB^2 + AC^2 = BC^2
21^2 + 28^2 = BC^2
BC^2 = 1225
BC = 35
ta có
\(BC^2=AB^2+AC^2=\frac{\left(AC+AB\right)^2}{2}+\frac{\left(AC-AB\right)^2}{2}=\frac{49^2+7^2}{2}=1225\)
Vậy \(BC=\sqrt{1225}=35cm\)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: \(BM=\sqrt{AB^2+AM^2}=25\left(cm\right)\)
CM=AC-AM=25(cm)
Xét ΔBMC có MB=MC
nên ΔMBC cân tại M
c: \(\widehat{ABC}=50^0\)
Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên trái: AH = 7cm; HC = 2cm
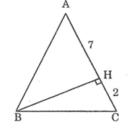
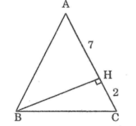

Tam giác ABC cân tại A ta có: AB = AC = CH + HA = 2 + 7 =9
Trong tam giác vuông BHA, ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=92-72=81-49=32
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2 mà BH2 = 32, HC2 = 22 = 4
BC2 =32 + 4 =36 ⇒ BC = √36 = 6 cm

Xét ΔABC có
AC-AB<BC<AB+AC
\(\Leftrightarrow7-3< BC< 7+3\)
\(\Leftrightarrow4< BC< 10\)
\(\Leftrightarrow BC\in\left\{5;7\right\}\)
Ta có: AC + AB > BC > AC - AB(bất đẳng thức tam giác)
=>7 + 3 > BC > 7 - 3
10 > BC > 4
Mà độ dài BC là số nguyên tố nên BC\(\in\)(5,7)
Với BC =5 thì \(\Delta ABC\) là tam giác thường
Với BC =7 thì \(\Delta ABC\) là tam giác cân
14 cm2
\(\sqrt{48}\)mới đúng