Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: ^BAH = ^BCA (vì 2 góc này cùng phụ với ^B)
Mà: ^MAC = ^BCA (tg MAC cân tại M vì Tg ABC vuông tại A có AM là trung tuyến)
Nên: ^BAH = ^MAC (4)
b) Tg AMD cân tại M (vì MA=MD) => ^D = ^DAM (1)
Ta có: MD//AH ( vì MD_I_ HM, AH _I_ HM )
Nên: ^D = ^DAH (2)
(1)(2) => ^DAM = ^DAH (3) => AD là p/g của ^HAM (5)
(3)(4) => ^BAH + ^DAH = ^MAC + ^DAM <=> ^BAD=^CAD => AD là p/g của ^BAC (6)
(5)(6) => AD là p/g chung của ^HAM và ^BAC
c) Ta có: AEDF là hcn ( vì ^E=^F=^A=90o )
Mà: AD là p/g của ^EAC (cmt)
Nên: AEDF là hình vuông
d) Tg DBE (^DEA=90o) và tg DCF (^DFC=90o) có:
DE = DF (AEDF là hình vuông)
DB = DC (MD là đường trung trực của BC)
Nên: Tg DBE = tg DCF (ch-cgv)

a) B A H ^ + M A C ^ vì cùng phụ với A B C ^
b) A 1 ^ = C 1 ^ (1) (chứng minh a)
Mà DABC vuông có AM là trung tuyến nên DAMC cân tại M C 1 ^ = A 4 ^ (2).
Từ (1) và (2) suy ra A 1 ^ = A 4 ^ (3)
D thuộc đường trung trực của BC.
Þ DM ^ BC = {M}
Þ D 1 ^ = A 2 ^
Vì DM = MA (giả thiết) ⇒ M 1 ^ = A 3 ^ ⇒ A 2 ^ = A 3 ^ (4)
Từ (3) và (4) Þ AD là phân giác chung của M A H ^ & C A B ^
c) Theo cách vẽ và kết quả câu b), ta có AEDF là hình vuông.
d) DDBE = DDCF (cạnh huyền - cạnh góc vuông)
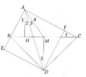

a) Ta có: ^BAH = ^BCA (vì 2 góc này cùng phụ với ^B)
Mà: ^MAC = ^BCA (tg MAC cân tại M vì Tg ABC vuông tại A có AM là trung tuyến)
Nên: ^BAH = ^MAC (4)
b) Tg AMD cân tại M (vì MA=MD) => ^D = ^DAM (1)
Ta có: MD//AH ( vì MD_I_ HM, AH _I_ HM )
Nên: ^D = ^DAH (2)
(1)(2) => ^DAM = ^DAH (3) => AD là p/g của ^HAM (5)
(3)(4) => ^BAH + ^DAH = ^MAC + ^DAM <=> ^BAD=^CAD => AD là p/g của ^BAC (6)
(5)(6) => AD là p/g chung của ^HAM và ^BAC
c) Ta có: AEDF là hcn ( vì ^E=^F=^A=90o )
Mà: AD là p/g của ^EAC (cmt)
Nên: AEDF là hình vuông
d) Tg DBE (^DEA=90o) và tg DCF (^DFC=90o) có:
DE = DF (AEDF là hình vuông)
DB = DC (MD là đường trung trực của BC)
Nên: Tg DBE = tg DCF (ch-cgv)

a: Xét tứ giác HCQB có
M là trung điểm của BC
M là trung điểm của HQ
Do đó: HCQB là hình bình hành

a) xét ▲ABD VÀ▲ EBD có
BD là cạnh chung
góc ABD= góc DBE
AB= BE
nên Δ ABD=Δ EBD (c.g.c)
b) vì Δ ABD=Δ EBD (cmt)
→ góc BED= góc BAC (2 góc tương ứng)
c) ta có:
AH VUÔNG VỚI BC
→ góc AHE = 90o (1)
góc bed = 90o (cmt) (2)
từ (1) và (2) suy ra DE song song với AH (2 đường thẳng cùng vuông góc với 1 đường thẳng)