Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét tam giác AOD và tam giác BOD có:
OA=OB (gt)
góc AOD= góc BOD ( OD là phân giác góc O)
OD chung
suy ra: tam giác AOD= BOD ( c.g.c)
suy ra: DA=DB (hai cạnh tương ứng)
b, vì tam giác AOD=BOD (chứng minh trên)
suy ra: góc ADO=gócBDO (2 góc tương ứng)
mà góc ADO+BDO=180 độ ( kề bù)
suy ra: góc ADO=góc BDO=180/2=90 độ (t/c)
suy ra: OD vuông góc với AB tại D (t/c)
Chúc bạn chơi game vui vẻ 🙂 và theo dõi tin tức game trên thegioigame.vn

Ta có hình vẽ
O A B D a/ Xét tam giác OAD và tam giác OBD có:
góc AOD = góc BOD (GT)
AD: cạnh chung
OA = OB (GT)
Vậy tam giác OAD = tam giác OBD (c.g.c)
=> DA = DB (2 cạnh tương ứng) (đpcm)
b/ Ta có: tam giác OAD = tam giác OBD (câu a)
=> góc ODA = góc ODB (2 góc tương ứng)
Mà góc ODA + góc ODB = 1800 (kề bù)
=> góc ODA = góc ODB = 1800 / 2 = 900
Vậy OD \(\perp\) AB (đpcm)

a, xét tam giác AOD và tam giác BOD có:
OA=OB (gt)
góc AOD= góc BOD ( OD là phân giác góc O)
OD chung
suy ra: tam giác AOD= BOD ( c.g.c)
suy ra: DA=DB (hai cạnh tương ứng)
b, vì tam giác AOD=BOD (chứng minh trên)
suy ra: góc ADO=gócBDO (2 góc tương ứng)
mà góc ADO+BDO=180 độ ( kề bù)
suy ra: góc ADO=góc BDO=180/2=90 độ (t/c)
suy ra: OD vuông góc với AB tại D (t/c)

Hình bạn tự vẽ nha!!!
a, Vì \(\Delta AOB\) có OA = OB (gt) => \(\Delta AOB\) cân tại O
Xét \(\Delta OAD\) và \(\Delta OBD\)
Có: OA = OB (gt)
\(\widehat{AOD}=\widehat{BOD}\) ( gt )
OD chung
=> \(\Delta OAD=\Delta OBD\left(c.g.c\right)\)
=> DA = DB ( 2 cạnh t/ứng )
b, Xét \(\Delta HOD\) và \(\Delta KOD\)
Có: OD chung
\(\widehat{HOD}=\widehat{KOD}\) (gt)
\(\widehat{DHO}=\widehat{DKO}\left(=90^0\right)\)
=> \(\Delta HOD=\Delta KOD\left(ch.gn\right)\)
=> DH = DK ( 2 cạnh t/ứng )
c, Ta có : \(\widehat{ODA}+\widehat{ODB}=\widehat{ADB}=180^0\) ( 2 góc kề bù )
Vì \(\Delta OAD=\Delta OBD\left(cmt\right)\)
=> \(\widehat{ODA}=\widehat{ODB}\) ( 2 góc t/ứng )
=> \(\widehat{ODA}=\widehat{ODB}=90^0\)
=> \(OD\perp AB\left(đpcm\right)\)
d, Vì \(\Delta ODA=\Delta ODB\left(cma\right)\)
=> AD = BD (2 cạnh t/ứng)
=> D là trung điểm AB
=> AD = BD = AB : 2 = 16 : 2 = 8 cm
Xét \(\Delta ODA\) vuông:
=> OD2 + AD2 = OA2 ( đ/lí Pytago )
Thay số: OD2 + 82 = 202
OD2 = 202 - 82
OD2 = 336
=> OD = \(\sqrt{336}\) cm
Vậy...


a) Xét \(\Delta AOD \) và \(\Delta BOD \) có:
\(\widehat{O_1}=\widehat{O_2}\) (gt)
OD là cạnh chung
OA = OB (gt)
Vậy \(\Delta AOD = \Delta BOD\) (c.g.c)
=> DA = DB (2 cạnh tương ứng)
b) Vì \(\Delta AOD = \Delta BOD\) nên \(\widehat{ADO}=\widehat{BDO}\) (2 góc tương ứng) (1)
Ta có: \(\widehat{AOD}\) kề bù với \(\widehat{BOD}\) nên \(\widehat{AOD}+\widehat{BOD}=180^0\) (2)
Từ (1) và (2) suy ra: \(\widehat{AOD}=\widehat{BOD}=\dfrac{180^0}{2}=90^0\)
=> OD \(\perp\) AB tại D.

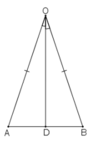
Xét ΔAOD và ΔBOD, ta có:
OA = OB (gt)
∠(AOD) = ∠(BOD)(vì OD là tia phân giác)
OD cạnh chung
Suy ra: ΔAOD= ΔBOD(c.g.c)
Vậy: DA = DB (hai cạnh tương ứng)

Ta có hình vẽ:
O A B D Xét tam giác OAD và tam giác OBD có:
OA = OB (GT)
\(\widehat{AOD}\)=\(\widehat{BOD}\) (GT)
OD: cạnh chung
=> tam giác OAD = tam giác OBD (c.g.c)
=> \(\widehat{ODA}\)=\(\widehat{ODB}\) (2 góc tương ứng)
Mà \(\widehat{ODA}\)+\(\widehat{ODB}\) = 1800 (kề bù)
=> \(\widehat{ODA}\)=\(\widehat{ODB}\) = 900
Vậy OD \(\perp\)AB (đpcm)
Ta có hình vẽ sau:
1 2 A O B D
Xét ΔOAD và ΔOBD có:
OD là cạnh chung
\(\widehat{O_1}=\widehat{O_2}\) (gt)
OA = OB (gt)
=> ΔOAD = ΔOBD (c-g-c)
=> \(\widehat{ADO}=\widehat{BDO}\) (2 góc tương ứng)
mà \(\widehat{ADO}+\widehat{BDO}=180^o\) (2 góc kề bù)
=> \(\widehat{ADO}=\widehat{BDO}\) = \(\frac{180^o}{2}\) = 90o
=> OD \(\perp\) AB (đpcm)


O A B D
xét \(\Delta OAB\)là \(\Delta\)cân vì \(OA=OB\)( giả thiết)
và \(OD\)là tia phân giác \(\widehat{AOB}\)cắt \(AB\)TẠI \(D\)
\(\Rightarrow OD\)ĐỒNG THỜI LÀ ĐƯỜNG TRUNG TRỰC CỦA \(\Delta OAB\)
\(\Rightarrow AD=DB\) và \(OD\perp AB\)tại \(D\)( điều phải chứng minh)
vậy \(AD=DB\) và \(OD\perp AB\)