Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)

Xét 2 tam giác vuông AMC và AMB có:
AM chung
BM=CM (gt)
=>\(\Delta AMC = \Delta AMB\) (hai cạnh góc vuông)
=> AC=AB (2 cạnh tương ứng)
=> Tam giác ABC cân tại A
b)

Kẻ MH vuông góc với AB (H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGM có:
AM chung
\(\widehat {HAM} = \widehat {GAM}\) (do AM là tia phân giác của góc BAC)
=>\(\Delta AHM = \Delta AGM\) (cạnh huyền – góc nhọn)
=> HM=GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM (giả thiết)
MH=MG(chứng minh trên)
=>\(\Delta BHM = \Delta CGM\)(cạnh huyền – cạnh góc vuông)
=>\(\widehat {HBM} = \widehat {GCM}\)(2 góc tương ứng)
=>Tam giác ABC cân tại A.

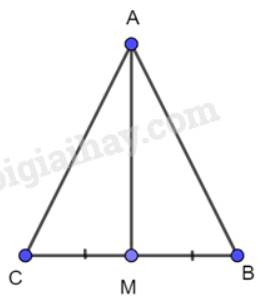
Xét 2 tam giác AMB và AMC có:
AM chung
AB=AC (do tam giác ABC cân tại A)
MB=MC (gt)
\(\Rightarrow\) \(\Delta AMB=\Delta AMC\) (c.c.c)
\(\Rightarrow\) \(\widehat {BAM} = \widehat {CAM}\)(2 góc tương ứng).
Mà tia AM nằm trong góc BAC
\(\Rightarrow\) AM là phân giác của góc BAC
Mặt khác: Do \(\Delta AMB=\Delta AMC\) nên \(\widehat {AMB} = \widehat {AMC}\)(2 góc tương ứng) mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
Nên: \(\widehat {AMB} = \widehat {AMC} = {90^o}\).
Vậy AM vuông góc với BC.

Xét \(\Delta ABC\)có
AM là đường trung tuyến ( M là trung điểm của BC )
AM là đường phân giác ( AM là tia phân giác của \(\widehat{BAC}\))
Nên \(\Delta ABC\)cân tại A ( tam giác có đường trung tuyến đồng thời là đường phân giác )

Tham khảo:
Xét tam giác `ABM` và tam giác `AMC`, ta có :
AM cạnh huyền chung
\(\widehat{AMB}=\widehat{AMC}=90^o\)(góc vuông )
\(\widehat{BAM}=\widehat{MAC}\)(giả thiết)
Do đó tam giác `ABM`=tam giác `AMC`(cạnh huyền-cạnh góc vuông)
\(=>AB=AC\)(hai cạnh tương ứng)
=>tam giác `ABC` cân tại `A.`

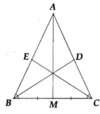
a) Chứng minh được ∆ A M B = ∆ A M C (c.c.c).
Từ đó suy ra AM là tia phân giác của góc BAC.
b) Xét tam giác ABC có AM, BD,CE là các tia phân giác. Từ tính chất ba đường phân giác trong tam giác, suy ra ba đường thẳng AM,BD,CE đồng quy.

Trên tia đối tia MA lấy N sao cho AM=MN=> ABNC là hình bình hành=> AB=CN và ^N=ˆBAN=ˆCAN→AC=CNN^=BAN^=CAN^→AC=CN
=> AB=AC => ĐPCM
-Cách 2: -Kẻ MH vuông góc với AB; MK vuông góc với AC( H thuộc AB và K thuộc AC).
-Ta có: tam giác AHM= tam giác AKM( cạnh huyền-góc nhọn).
=> HM=MK. => tam giác BHM= tam giác CKM( cạnh huyền-cạnh góc vuông).
=> góc HBM= góc KCM. => tam giác ABC cân tại A.(đpcm)
Trên tia đối tia MA lấy điểm I sao cho MI=MA
Bạn tự ghi góc ra nha
Xét tam giác BMA và tam giác CMI ta có:
MB=MC(GT)
BMA=IMC(đối đỉnh)
MA=MI(GT)
\(\Rightarrow\) tam giác BMA=CMI(c.g.c)
BA=IC(cặp cạnh tương ứng)
BAM=MIC(cặp góc tương ứng)
Mà BAM=CAM nên CAM=CIM
Suy ra tam giác CAI là tam giác cân
Suy ra CA=CI
Mà CI=BA
Suy ra BA=AC
Vậy tam giác ABC cân