Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chứng minh D E A ^ = 180 0
b) Chứng minh
A I M ^ = A K M ^ = I A K ^ = 90 0
c) Chứng minh DDME có E D M ^ = D E M ^ = 45 0
Þ DDME vuông cân ở M.


a) Ta có A1 + C1 = 90 độ (...)
A3 + B1 = 90 độ (...)
=> A1 + A3 + C1 + B1 = 180 độ (1)
Có BD vuông góc DE
CE vuông góc DE
=> BD // EC
=> B1 + B2 + C2 + C1 = 180 độ
Mà B2 + C2 = 90 độ => B1 + C1 = 90 độ (2)
Từ (1) và (2) => A3 + A1 = 90 độ. Mà A2 = 90 độ
Suy ra : A1 + A2 + A3 = 180 độ. Hay góc DAE là góc bẹt
=> D,A,E thẳng hàng.
b) Ta có AM=MC
AE=EC
=> ME là đường trung trực của AC.
=> AKM = 90 độ (3)
CMTT => AIM = 90 độ (4)
Mà IAK = BAC = 90 độ (5)
Từ (3)(4)(5) => IMKA là hình chữ nhật
c) Có ME là đường trung trực của AC (câu b)
Mà ▲AEC vuông cân tại E => EM là tia phân giác AEC
=> AEM = 90/2 = 45 độ. (*)
Ta lại có IMKA là hình chữ nhật => IMK = 90 độ (**)
Từ (*) và (**) => ▲DME vuông cần tại M

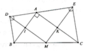
A B C D E M I K n
Hình ảnh chỉ mang t/c minh họa
a,Tam giác ABD vuông cân => \(\widehat{BAD}=\widehat{ABD}=45^{o}\)
Tam giác ACE vuông cân => \(\widehat{CAE}=\widehat{ACE}=45^{o}\)
=>\(\widehat{DAE}=\widehat{BAD}+\widehat{A}+\widehat{CAE}=45^{o}+90^{o}+45^{o}=180^{o}\)
=> 3 điểm A,D,E thẳng hàng
\(b, cm\Delta BID=\Delta AID=>\widehat{BID}=\widehat{AID}=90^{o}\\ =>\widehat{BIM}=\widehat{AIM}=90^{o}\\ cm \ tg \ tự \ ta \ có: \widehat{AKM}=\widehat{CKM}=90^{o}\\ \)
=>IAKM là hcn
c,Thep phần b có IAKM là hcn=> \(\widehat{DME}=90^{o}\)
Và \(\Delta BID=\Delta AID=>AI=BI\)
=>DI là đg trung tuyến mà tam giác DAB vuông cân
=> DI là đg phân giác=>\(\widehat{ADM}=45^{o}\)
Tg tự: \(\widehat{AEM}=45^{o}\)
=>Tam giác AME vuông cân