Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
b: Xet ΔDAF vuông tại A và ΔDEC vuông tạiE có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>DF=DC
c: AD=DE
mà DE<DC
nên AD<CD
d: Xét ΔBFC có BA/AF=BE/EC
nên AE//FC

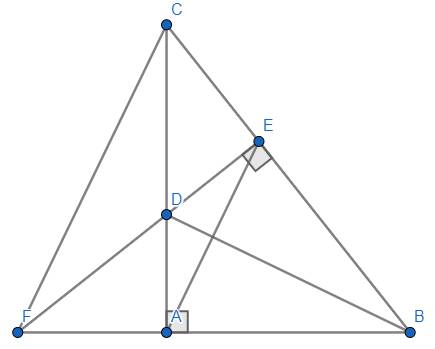
(a) Xét \(\Delta ABD,\Delta EBD:\left\{{}\begin{matrix}\hat{BAD}=\hat{BED}=90^o\left(gt\right)\\\text{BD chung}\\\hat{EBD}=\hat{ABD}\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABD=\Delta EBD\left(c.h-g.n\right)\Rightarrow\left\{{}\begin{matrix}BA=BE\\DA=DE\end{matrix}\right.\)
\(\Rightarrow BD\) là đường trung trực của \(AE\left(đpcm\right).\)
(b) Xét \(\Delta ADF,\Delta EDC:\left\{{}\begin{matrix}\hat{DAF}=\hat{DEC}=90^o\left(gt\right)\\AD=DE\left(cmt\right)\\\hat{ADF}=\hat{EDC}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ADF=\Delta EDC\left(g.c.g\right)\Rightarrow AF=CE.\)
Lại có: \(BA=BE\left(cmt\right)\Rightarrow BA+AF=BE+CE\Leftrightarrow BC=BF\)
\(\Rightarrow\Delta BCF\) cân tại \(B.\)
Ta cũng có: \(\left\{{}\begin{matrix}FE\perp BC\\CA\perp BF\\FE\cap CA=\left\{D\right\}\end{matrix}\right.\Rightarrow BD\) là đường cao thứ ba của \(\Delta BCF\Rightarrow BD\) vừa là đường cao, vừa là đường trung trực của \(CF\Rightarrow DC=DF\left(đpcm\right).\)

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E

a) ΔABD và ΔEBD có:
BA = BE (gt)
B1ˆ=B2ˆ (BD là tia phân giác góc B)
BD là cạnh chung
⇒ΔABD=ΔEBD (c.g.c)
⇒⇒ BADˆ=BEDˆ(hai góc tương ứng)
mà BAD^ =90 độ
⇒BEDˆ= 90 độ
⇒ DE ⊥⊥ BE
b) ΔABI và ΔEBIcó:
BA = BE (gt)
B1ˆ=B2ˆ (gt)
BI là cạnh chung
⇒ΔABI=ΔEBI (c.g.c)
⇒ IA = IE (hai cạnh tương ứng) (1)
Ta có: I1ˆ+I2ˆ=1800 (hai góc kề bù)
mà I1ˆ=I2ˆ (ΔABI=ΔEBI)
⇒ I1ˆ=I2ˆ=90 độ (2)
Từ (1) và (2) ⇒⇒ DE vuông góc với BE.
c) ΔAHE vuông tại H có góc AEH nhọn
⇒góc AEC là góc tù
⇒⇒ AHEˆ<AECˆ
⇒⇒ AE < AC (quan hệ giữa cạnh và góc đối diện)
mà EH là hình chiếu của AE trên BC.
HC là hình chiếu của AC trên BC.
⇒⇒ EH < HC (quan hệ đường xiên và hình chiếu
giúp mình bài toán này với