Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ABCH??20cm16 cm9 cm
Lg
*Áp dụng định lý py-ta-go ta có: (Δ AHC)
AC2=AH2+HC2
202=AH2+162
400=AH2+256
AH2=144
AH=√144 =12
*Áp dụng định lý py-ta-go ta có: (Δ AHB)
AB2=AH2+BH2
AB2=122+92
AB2=225
AB=√225 =15

Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm

A B C H
XÉT \(\Delta BAH\)VUÔNG TẠI H
CÓ \(AB^2=BH^2+HA^2\left(Đ/L,PY-TA-GO\right)\)
THAY\(5^2=BH^2+4^2\)
\(\Rightarrow BH^2=5^2-4^2\)
\(\Rightarrow BH^2=25-16\)
\(\Rightarrow BH^2=9\)
\(\Rightarrow BH=\sqrt{9}=3\left(cm\right)\)
TA CÓ \(BH+HC=BC\)
THAY\(3+12=BC\)
\(BC=15\left(cm\right)\)
XÉT \(\Delta HAC\)VUÔNG TẠI H
CÓ \(AC^2=AH^2+HC^2\)(Đ/L PYTAGO)
THAY\(AC^2=4^2+12^2\)
\(AC^2=16+144\)
\(AC^2=160\)
\(\Rightarrow AC=\sqrt{160}=4\sqrt{10}\)
CHU VI \(\Delta ABC\)LÀ
\(AB+AC+BC=5+4\sqrt{10}+15=20+4\sqrt{10}\)

Vẽ hình ra thì nó " siêu to khổng lồ " lắm :)
Ta có : BC = BH + HC = 9 + 16 = 25cm
Áp dụng định lí Pytago cho tam giác vuông ABC có :
BC2 = AB2 + AC2
AB = \(\sqrt{25^2-20^2}=15cm\)
Áp dụng định lí Pytago cho tam giác vuông ABH có :
AB2 = BH2 + AH2
AH = \(\sqrt{15^2-9^2}=12cm\)
Vậy AB = 15cm , AH = 12cm

BC=25cm
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
=>AC=20cm

△ABC vuông tại A có \(BC^2=AB^2+AC^2\\ \Rightarrow BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(\Rightarrow CH=BC-BH=25-9=16\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=15^2+20^2=625\)
hay BC=25(cm)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=25-9=16(cm)
Vậy: CH=16cm

A B C H 20 cm 9cm 16 cm
*) Áp dụng định lí Pythagoras vào \(\Delta\)vuông ACH, ta có :
\(\Rightarrow\)AC2 = HC2 + AH2
\(\Rightarrow\)202 = 162 + AH2
\(\Rightarrow\)AH2 = 400 - 256
\(\Rightarrow\)AH2 = 144
\(\Rightarrow\)AH = 12 (cm)
*) Áp dụng định lí Pythagoras vào \(\Delta\)vuông ABH, ta có :
\(\Rightarrow\)AB2 = AH2 + HB2
\(\Rightarrow\)AB2 = 122 + 92
\(\Rightarrow\)AB2 = 225
\(\Rightarrow\)AB = 15 (cm)
Vậy AB = 15 cm; AH = 12 cm

Xét △BHC vuông tại H có: BH2 + HC2 = BC2 (định lý Pytago)
=> BH2 + 162 = 202
=> BH2 = 202 - 162 = 400 - 256 = 144
=> BH = 12 (cm)
Xét △BHA vuông tại H có: BH2 + AH2 = AB2 (định lý Pytago)
=> 122 + 92 = AB2
=> AB2 = 144 + 81 = 225
=> AB = 15 (cm)
Ta có: AC = AH + HC = 9 + 16 = 25
Xét △ABC có:
AC2 = 252 = 625
AB2 + BC2 = 152 + 202 = 225 + 400 = 625
=> AC2 = AB2 + AC2
=> △ABC vuông tại A
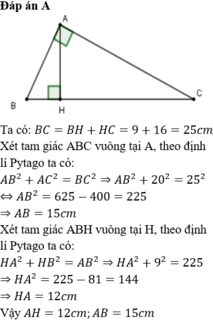
Ta có : BC = BH + HC = 9 + 16 = 25 (cm)
Tam giác ABC vuông tại A nên :
BC2 = AB2 + AC2
252 = AB2 + 162
=> AB2 = 252 - 202
AB2 = 625 - 400 = 225 = 152
=> AB = 15 (cm)
Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = AH2 + 162
=> AH2 = 202 - 162
AH = 400 - 256 = 144 = 122
=> AH = 12 (cm)
Vậy AB = 15 cm ; AH = 12 cm
Tham khảo link này nek:
https://h.vn/hoi-dap/question/168012.html
# mui #