Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

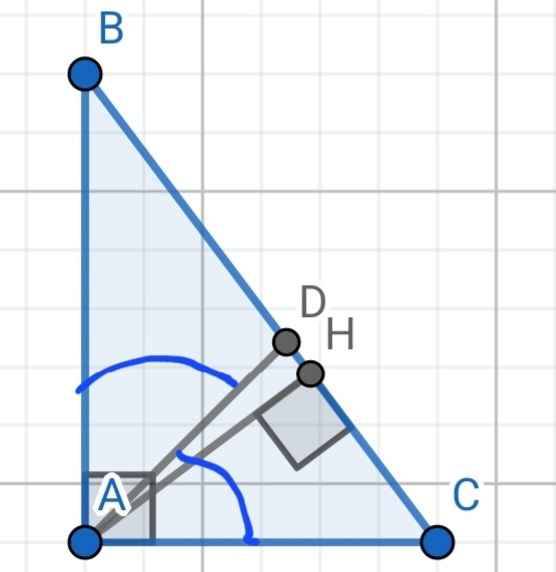
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA

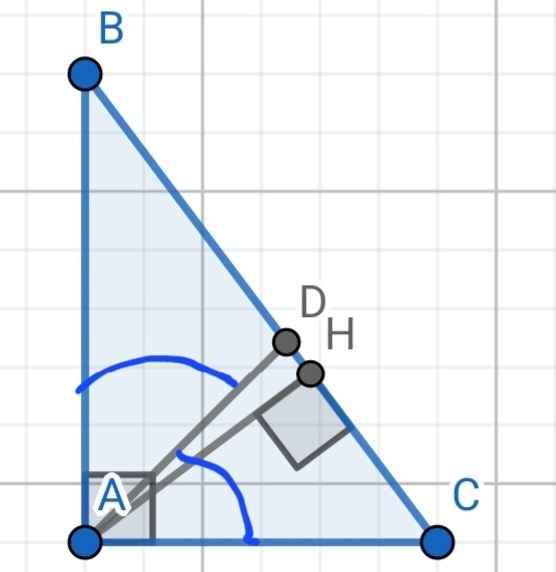
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA
a: DB/DC=AB/AC=4/3
b: Sửa đề: AH/CA=AB/BC
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)
=>AH*BC=AB*AC
=>AH/AC=AB/CB

a) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{DB}{DC}=\dfrac{6}{8}=\dfrac{3}{4}\)

1 2 B D H C A (Bonus thêm cho cái hình :>>)
a) Ta có: AD là tia phân giác của góc BAC
\(\Rightarrow\frac{AB}{AC}=\frac{DB}{DC}\)
\(\Leftrightarrow\frac{DB}{DC}=\frac{8}{6}\)
\(\Rightarrow\frac{DB}{DC}=\frac{4}{3}\)
b) Ta có: \(\widehat{B_1}+\widehat{C_1}=90^o\left(\Delta ABC\text{ vuông}\right)\)
\(\widehat{C_1}+\widehat{HAC}=90^o\left(\Delta AHC\text{ vuông}\right)\)
\(\Rightarrow\widehat{B_1}=\widehat{HAC}\left(=\widehat{C_1}\right)\)
Xét \(\Delta AHB\text{ và }\Delta CHA\)
Có: \(\widehat{AHC}=\widehat{AHB}\left(=90^o\right)\)
\(\widehat{B_1}=\widehat{HAC}\)
\(\Rightarrow\Delta AHB~\Delta CHA\)
c) Xét tam giác ABC vuông tại A
<=> BC^2= AB^2+AC^2(áp dụng định lí Py-ta-go)
<=> BC^2= 100
<=> BC= 10 (cm)
Xét tam giác AHB ~ tam giác CHA (chứng minh trên)
<=> AH/CA= AB/CB
<=> AH= AB.CA /CB
<=> AH = 8.6 : 10 = 4,8 (cm)
Xét tam giác AHB vuông tại H
=> BH^2= AB^2-AH^2= 8^2-4,8^2=40,96
=> BH= 6,4 cm
Xét tam giác CHA vuông tại H
=> CH^2=AC^2-AH^2=6^2-4,8^2=12,96
=> CH = 3,6 cm
Ta có:
S.AHB / S.CHA = (1/2 . BH.HA )/ (1/2 . HC .AH)
= BH / HC = 6,4 / 3,6 =16/9

a: BC=căn 6^2+8^2=10cm
AD là phân giác
=>BD/CD=AB/AC=3/4
=>BD/3=CD/4=(BD+CD)/(3+4)=10/7
=>BD=30/7cm
b: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA

a) \(\Delta ABC\) có \(AD\) là phân giác \(\widehat{BAC}\) theo tính chất đường phân giác của tam giác ta có:
\(\frac{BD}{AB}=\frac{DC}{AC}\) \(\Rightarrow\)\(\frac{DB}{DC}=\frac{AB}{AC}\)
hay \(\frac{DB}{DC}=\frac{8}{6}=\frac{4}{3}\)
b) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\) cm
mà \(\frac{DB}{DC}=\frac{4}{3}\)\(\Rightarrow\) \(\frac{DB}{4}=\frac{DC}{3}=\frac{DB+DC}{4+3}=\frac{BC}{7}=\frac{10}{7}\)
suy ra: \(DB=\frac{10}{7}.4\approx5,71\)
\(DC=\frac{10}{7}.3\approx4,29\)

a: DB/DC=AB/AC=8/6=4/3
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
Câu 4(Son Cho A ABC vuông ti A, đường phân các ID DE HC (E in BC ) i đừng thẳng Dễ cắt đường thẳng AB tại E. a) Chung minh BD LCF b) Chứng minh Ff= FCDw i triangle FBF- triangle FDC. c) Tính tỉ số diện tích của SHIID vì AABC bởi AB = 9cmc AC = 12cm