Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔADE đồng dạng với ΔABC
góc ADE=góc ABC, góc AED=góc ACB
k=AD/AB=2/5
b: DE//BC
=>AD/AB=DE/BC
=>DE/6,5=2/5
=>DE=2,6cm

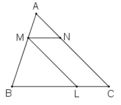
A B C M N L
a, Tam giác ABC có MN // BC \(\left(M\in AB;N\in AC\right)\)=> Tam giác AMN 
Tam giác ABC có ML // AC \(\left(M\in AB;L\in BC\right)\)=> Tam giác MBL 
Tam giác AMN 


b, Tam giác AMN 
\(\widehat{A} chung ,\widehat{AMN}=\widehat{B} ; \widehat{ANC}=\widehat{C}\)
\(\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)
Tỉ số đồng dạng \(k=\frac{AM}{AB}=\frac{1}{3}\)( Vì AM = \(\frac{1}{2}\)MB )
Tam giác AMN
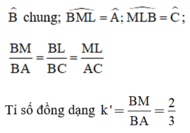
\(\widehat{B}\)chung ; \(\widehat{BML}=\widehat{A}\); \(\widehat{MLB}=\widehat{C}\)
\(\frac{BM}{BA}=\frac{BL}{BC}=\frac{ML}{AC}\)
Tỉ số đồng dạng \(k'=\frac{BM}{BA}=\frac{2}{3}\)
Tam giác AMN 
\(\widehat{AMN}=\widehat{B};\widehat{ANM}=\widehat{BLM};\widehat{A}=\widehat{BLM}\)
\(\frac{AM}{MB}=\frac{AN}{ML}=\frac{MN}{BL}\)
=> Tiwr số đồng dạng \(k''=\frac{AM}{MB}=\frac{1}{2}\)

a) ΔABC có MN // BC (M ∈ AB; N ∈ AC) ⇒ ΔAMN  ΔABC.
ΔABC.
ΔABC có ML // AC (M ∈ AB; L ∈ BC) ⇒ ΔMBL  ΔABC
ΔABC
ΔAMN  ΔABC; ΔMBL
ΔABC; ΔMBL  ΔABC ⇒ ΔAMN
ΔABC ⇒ ΔAMN  ΔMBL.
ΔMBL.
b) ΔAMN  ΔABC có:
ΔABC có:
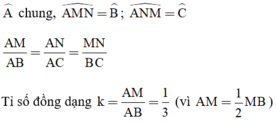
ΔMBL 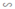 ΔABC có:
ΔABC có:
ΔAMN 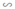 ΔMBL có:
ΔMBL có:
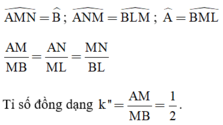

Bài này là: Bài 27 trang 72 Toán 8 Tập 2 đúng không bạn
a) \(\Delta ABC\) có \(MN\) // \(BC\) \(\left(M\in AB;N\in AC\right)\Rightarrow\Delta AMN\sim\Delta ABC\) (định lí)
\(\Delta ABC\) có \(ML\) // \(AC\) \(\left(M\in AB;L\in BC\right)\Rightarrow\Delta MBL\sim\Delta ABC\) (định lí)
Vì \(\Delta AMN\sim\Delta ABC\) và \(\Delta MBL\sim\Delta ABC\)
\(\Rightarrow\Delta AMN\sim\Delta MBL\)
b) Xét \(\Delta AMN\sim\Delta ABC\) có:
\(\widehat{A}\) chung
\(\widehat{AMN}=\widehat{B};\widehat{ANM}=\widehat{C}\)
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\)
Tỉ số đồng dạng : \(k=\dfrac{AM}{AB}=\dfrac{1}{2}\left(AM=\dfrac{1}{2}MB\right)\)
Xét \(\Delta MBL\sim\Delta ABC\) có:
\(\widehat{B}\) chung
\(\widehat{BML}=\widehat{A};\widehat{MLK}=\widehat{C}\)
\(\dfrac{BM}{BA}=\dfrac{BL}{BC}=\dfrac{ML}{AC}\)
Tỉ số đồng dạng: \(k'=\dfrac{BM}{BA}=\dfrac{2}{3}\)
Xét \(\Delta AMN\sim\Delta MBL\) có:
\(\widehat{AMN}=\widehat{B};\widehat{ANM}=\widehat{BLM};\widehat{A}=\widehat{BML}\)
\(\dfrac{AM}{MB}=\dfrac{AN}{ML}=\dfrac{MN}{BL}\)
Tỉ số đồng dạng: \(k''=\dfrac{AM}{MB}=\dfrac{1}{2}\)

a) MN // BC => ∆AMN ∽ ∆ABC
ML // AC => ∆MBL ∽ ∆ABC
và ∆AMN ∽ ∆MLB
b)
∆AMN ∽ ∆ABC có:
ˆAMNAMN^ = ˆABCABC^; ˆANMANM^ = ˆACBACB^
AMABAMAB= 1313
∆MBL ∽ ∆ABC có:
ˆMBLMBL^ = ˆBACBAC^, ˆBB^ chung, ˆMLBMLB^ = ˆACBACB^
MBABMBAB= 2323
∆AMN ∽ ∆MLB có:
ˆMANMAN^ = ˆBMLBML^, ˆAMNAMN^ = ˆMBLMBL^, ˆANMANM^ = ˆM

a: ΔCEF đồng dạng với ΔCAB theo tỉ số k=CE/CA
ΔADE đồng dạng với ΔABC
=>k'=AD/AB=2/5
b: \(\dfrac{C_{ADE}}{C_{ABC}}=\dfrac{AD}{AB}=\dfrac{2}{5}\)
=>\(C_{ADE}=\dfrac{2}{5}\cdot\left(5+7+9\right)=\dfrac{2}{5}\cdot21=\dfrac{42}{5}\left(cm\right)\)
ΔCEF đồng dạng với ΔCAB
=>\(\dfrac{C_{CEF}}{C_{CAB}}=\dfrac{CE}{CA}=\dfrac{3}{5}\)
=>\(C_{CEF}=\dfrac{3}{5}\cdot\left(5+7+9\right)=\dfrac{3}{5}\cdot21=\dfrac{63}{5}\left(cm\right)\)
