K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 9 2021
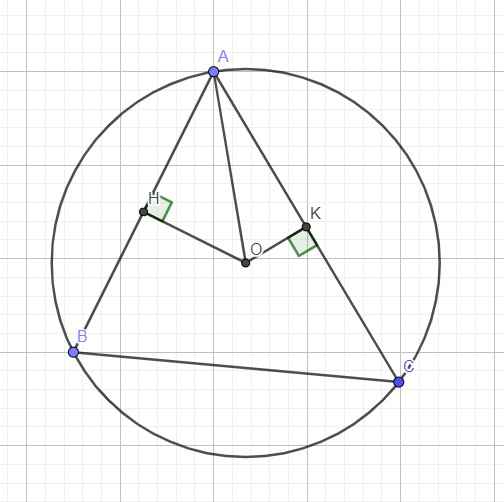
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) \(\Rightarrow OH=2\sqrt{2}\)
Áp dụng định lý Pitago cho tam giác OAH:
\(AH=\sqrt{OA^2-OH^2}=\sqrt{3^2-\left(2\sqrt{2}\right)^2}=1\)
\(\Rightarrow AB=2AH=2\left(cm\right)\)
Gọi K là trung điểm AC \(\Rightarrow OK\perp AC\Rightarrow OK=\dfrac{\sqrt{11}}{2}\)
Áp dụng định lý Pitago cho tam giác AOK:
\(AK=\sqrt{OA^2-OK^2}=\sqrt{3^2-\left(\dfrac{\sqrt{11}}{2}\right)^2}=2,5\left(cm\right)\)
\(\Rightarrow AC=2AK=5\left(cm\right)\)

30 tháng 5 2018
Tìm ba phân số khác nhau biết phân số thứ nhất và phân số thứ hai là 7/8,tổng của phân số thứ hai và phân số thứ ba là 8/7,tổng của phân số thứ nhất và phân số thứ ba là 8/9
Lời giải:
Kẻ $OM, ON$ lần lượt vuông góc với $AB, AC$
Vì $OAB$ là tam giác cân tại $O$ ($OA=OB=R=3$) nên đường cao $OM$ đồng thời là đường trung tuyến
$\Rightarrow M$ là trung điểm $AB$
Áp dụng định lý Pitago:
$MB=\sqrt{OB^2-OM^2}=\sqrt{3^2-(2\sqrt{2})^2}=1$
$\Rightarrow AB=2MB=2$ (cm)
Tương tự:
$N$ là trung điểm $AC$
$NC=\sqrt{OC^2-ON^2}=\sqrt{3^2-(\frac{\sqrt{11}}{2})^2}=2,5$ (cm)
$AC=2NC=2.2,5=5$ (cm)
Hình vẽ: