Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BẠN TỰ VẼ HÌNH NHÉ
a) Xét tam giác MCK và tam giác MBA
Có : CM = BM ( gt )
MK = MA ( gt )
Góc CMK = Góc BMA ( đối đỉnh )
Vậy tam giác MCK = tam giác MBA (c.g.c)
=> AB = CK (cạnh tương ứng )

Giả sử tam giác ABC vuông tại A óc góc B = 60 độ
Để AI = IM thì I là trung điểm của AM
=> BI là trung tuyến cũng là đường cao
=> tam giác ABM cân tại B có góc B = 60 độ
=> tam giác ABM đều
Tương tự cho MK và KD.
Vậy khi tam giác ABC vuông tại A với AB < AC và góc B = 60 độ thì AI = IM = MK = KD.

Mjk tra loi cau a nka
B C M K
Mjk ve hoi xau, pn thong cam nka
Vì tam giác ABM và ACM có:
M1=M2(đối đỉnh dok pn)
AM=MK(gt)
BM=MC( gt)
=> tam giác ABM=tam giác ACM(c.g.c)
k ve dc tam giac nho nen mjk phai ghi la tam giac lun ak

Lời giải:
a. Xét tam giác $AMC$ và $KMB$ có:
$MC=MB$ (do $M$ là trung điểm $BC$)
$AM=KM$ (gt)
$\widehat{AMC}=\widehat{KMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle KMB$ (c.g.c)
và $\widehat{ACM}=\widehat{KBM}$
Mà 2 góc này ở vị trí so le trong nên $AC\parallel BK$
b.
Xét tam giác $ABM$ và $KCM$ có:
$BM=CM$
$AM=KM$
$\widehat{AMB}=\widehat{KMC}$ (đối đỉnh)
$\Rightarrow \triangle ABM=\triangle KCM$ (c.g.c)
$\Rightarrow \widehat{ABM}=\widehat{KCM}$
Mà 2 góc này ở vị trí so le trong nên $AB\parallel CK$

a) Xét ∆ABM và ∆CME ta có :
BM = MC ( M là trung điểm BC)
AM = ME
AMB = CME ( đối đỉnh)
=> ∆ABM = ∆CME(c.g.c)
b) Xét ∆AMC và ∆BME ta có :
AM = ME
BM = MC
AMC = BME ( đối đỉnh)
=> ∆AMC = ∆BME(c.g.c)
=> ACM = MBE
Mà 2 góc này ở vị trí so le trong
=> AC//BE
c) Vì ∆AMB = ∆CME
=> ABC = BCK
Xét ∆IMB và ∆CMK ta có :
BM = MC
BI = CK
ABC = BCE (cmt)
=> ∆IMB = ∆CMK (c.g.c)
=> IMB = CMK
Ta có :
BMI + IMC = 180° ( kề bù)
Mà IMB = CMK
=> CMK + IMC = 180°
=> IMK = 180°
=> IMK là góc bẹt
=> I , M , K thẳng hàng
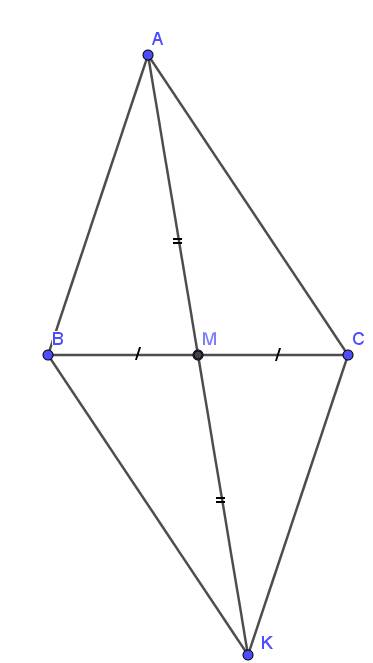
M A B C K
a, \(\Delta AMB\)và \(\Delta CMK\), ta có :
MB=MC ( vì M là chung điểm của BC)
Góc AMB = Góc CMK ( 2 góc đối đỉnh )
AM=MK
=> \(\Delta AMB=\Delta CMK\)( c.g.c)
=> AB=CK ( 2 cạnh tương ứng )
b, \(\Delta BMK\)và \(\Delta AMC\) ta có :
MB = MC
Góc BMK = Góc AMC ( 2 góc đối đỉnh )
AM = MK
=> \(\Delta BMK=\Delta AMC\)(c.g.c)
=> AC = BK ( 2 cạnh tương ứng )
c , Vì \(\Delta AMB=\Delta CMK\)
=> Góc BAM = góc MKC ( 2 góc tương ứng )
Mà góc BAM và góc MKC ở vị trí sole trong
=> AB//CK
d , Vì \(\Delta BMK=\Delta AMC\)
=> Góc BKM= góc MAC ( 2 góc tương ứng )
Mà góc BKM và Góc MAC ở vị trí sole trong
=> AC // BK