Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa lại đề bài: chỗ EN = ED fai là EN = EB ms đúng chứ nhỉ
Ta có hình vẽ:
A B C M N K E
a) Vì K là trung điểm của AB nên AK = KB
Xét Δ AKM và Δ BKC có:
AK = KB (cmt)
AKM = BKC (đối đỉnh)
KM = KC (gt)
Do đó, Δ AKM = Δ BKC (c.g.c)
=> AM = BC (2 cạnh tương ứng); AMK = BCK (2 góc tương ứng)
Mà AMK và BCK là 2 góc so le trong => AM // BC (đpcm)
b) Vì E là trung điểm của AC nên AE = EC
Xét Δ AEN và Δ CEB có:
AE = CE (cmt)
AEN = CEB (đối đỉnh)
EN = EB (gt)
Do đó, Δ AEN = Δ CEB (c.g.c)
=> AN = BC (2 cạnh tương ứng); ANE = CBE (2 góc tương ứng)
Mà ANE và CBE là 2 góc so le trong => AN // BC (đpcm)
c) Ta có: AM // BC (câu a)
AN // BC (câu b)
Mà theo tiên đề Ơ-clit qua 1 điểm nằm ngoài 1 đường thẳng chỉ vẽ được 1 đường thẳng song song với đường thẳng cho trước nên AM trùng với AN hay 3 điểm A, M, N thẳng hàng
Mặt khác, AM = BC = AN => A là trung điểm của MN (đpcm)

Giải:
Xét ΔAMK,ΔBCKΔAMK,ΔBCK có:
AK=KB(=12AB)AK=KB(=12AB)
K1ˆ=K2ˆK1^=K2^ ( đối đỉnh )
MK=KC(gt)MK=KC(gt)
⇒ΔAMK=ΔBCK(c−g−c)⇒ΔAMK=ΔBCK(c−g−c)
⇒A1ˆ=Bˆ⇒A1^=B^ ( góc t/ứng )
Xét ΔANE,ΔCBEΔANE,ΔCBE có:
AE=EC(=12AC)AE=EC(=12AC)
E1ˆ=E2ˆE1^=E2^ ( đối đỉnh )
BE=EN(gt)BE=EN(gt)
⇒ΔANE=ΔCBE(c−g−c)⇒ΔANE=ΔCBE(c−g−c)
⇒A2ˆ=Cˆ⇒A2^=C^ ( góc t/ứng )
Ta có: Aˆ+Bˆ+Cˆ=180oA^+B^+C^=180o ( tổng 3 góc của ΔABCΔABC )
⇒Aˆ+A1ˆ+A2ˆ=180o⇒A^+A1^+A2^=180o
⇒MANˆ=180o⇒MAN^=180o
⇒M,A,N⇒M,A,N thẳng hàng (1)
Vì ΔAMK=ΔBCKΔAMK=ΔBCK
⇒MA=BC⇒MA=BC ( cạnh t/ứng )
Vì ΔANE=ΔCBEΔANE=ΔCBE
⇒AN=BC⇒AN=BC
⇒MA=AN(=BC)⇒MA=AN(=BC) (2)
Từ (1) và (2) ⇒A⇒A là trung điểm của MN
Vậy A là trung điểm của MN

M A N B C K E
Xét \(\Delta AMKvà\Delta BKCcó:\)
KA=KB
góc MKA=góc BKC
KM=KC
\(\Rightarrow\Delta AMK=\Delta BCK\left(c-g-c\right)\)
\(\Rightarrow\)AM=BC (1)
\(\Rightarrow\)MA//BC (góc M so le trong với góc C) (3)
Xét \(\Delta AENvà\Delta BECcó:\)
EA=EC
góc AEN=góc BEC
EN=EB
\(\Rightarrow\Delta AEN=\Delta CEB\left(c-g-c\right)\)
\(\Rightarrow\)NA=BC (2)
\(\Rightarrow\)NA//BC (góc N so le trong với góc C) (4)
Từ (1) và (2) có: M,A,N thẳng hàng
Từ (3) và (4) có: AM=AN

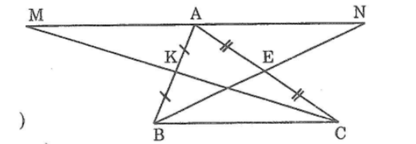
Xét ΔAKM và ΔBKC ta có:
AK = BK (Vì K là trung điểm AB)
∠(AKM) =∠(BKC) (đối đỉnh)
KM=KC (giả thiết)
Suy ra: ΔAKM = ΔBKC(c.g.c)
⇒AM =BC (hai cạnh tương ứng)
Và ∠(AMK) =∠(BCK) (2 góc tương ứng)
Suy ra: AM // BC ( vì có cặp góc so le trong bằng nhau)
Tương tự: ΔAEN= ΔCEB(c.g.c)
⇒ AN = BC (2 cạnh tương ứng)
Và ∠(EAN) =∠(ECB) (2 góc tương ứng)
Suy ra: AN // BC (vì có cặp góc so le trong bằng nhau)
Ta có: AM // BC và AN // BC nên hai đường thẳng AM và AN trùng nhau hay A,M,N thẳng hàng (1)
Lại có: AM = AN ( vì cùng bằng BC) (2)
Từ (1) và (2) suy ra: A là trung điểm của MN
