Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

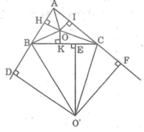
* Nếu O là điểm nằm trong ΔABC
Kẻ OH ⊥ AB, OK ⊥ BC, OI ⊥ AC
Vì điểm O cách đều các đường thẳng AB, BC, CA nên: OH = OK = OI
+) Ta có: OH = OK nên O nằm trên đường phân giác của góc ∠ABC.
Do OK = OI nên O nằm trên đường phân giác của góc ∠ACB
Do OH = OI nên O nằm trên đường phân giác của góc ∠BAC
Vậy O là giao điểm các đường phân giác trong của ΔABC
* Nếu O' nằm ngoài ΔABC
Kẻ O'D ⊥ AB, O'E ⊥ BC, O'F ⊥ AC
Vì O' cách đều ba đường thẳng AB, BC, AC nên: O'D = O'E = O'F
Vì O'D = O'F nên O' nằm trên tia phân giác của ∠(BAC)
Vì O'D = O'E nên O' nằm trên tia phân giác của ∠(DBC)
Suy ra O' là giao điểm phân giác trong của ∠(BAC) và phân giác ngoài tại đỉnh B.
Khi đó A, O, O' thẳng hàng ( vì hai tia AO và AO’ đều là tia phân giác của góc BAC) và A, H, D thẳng hàng
Ta có: OH < O'D
Vậy O là giao điểm các đường phân giác trong ΔABC cách đều ba đường thẳng AB, BC, CA và ngắn nhất.

Vẽ 3 tia phân giác của tam giác ABC, giao điểm của 3 tia phân giác chính là điểm cần tìm.

Trong tam giác, đường có độ dài ngắn nhất luôn là đường cao (đường vuông góc).
Vậy: khoảng cách từ D đến điểm A là nhỏ nhất khi \(AD \bot BC\).
Bước 1: Vẽ hai đường cao hạ từ đỉnh B và C.
Bước 2: Gọi H là giao điểm của hai đường cao.
Bước 3: Vẽ đường cao hạ từ H xuống BC. Và giao điểm của đường cao hạ từ H với đoạn thẳng BC là điểm D ta cần tìm.


I N B A K C M
Điểm cách đều các đường thẳng AB và AC nằm trên các đường phân giác (trong và ngoài) của góc B.
Điểm cách đều các đường thẳng AB và AC nằm trên các đường phân giác (trong và ngoài) của góc A.
Điểm cách đều các đường thẳng AB, BC, CA là giao điểm của các đường phân giác trên, đó là bốn điểm I, K, M, N.
Để khoảng cách nói trên là ngắn nhất, ta chọn điểm I, giao điểm của các đường phân giác trong của \(\Delta ABC.\)