Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A) MP vuông góc AB tại P => góc MPA=90; MQ vuông góc AC tại Q=> MQA=90
=> tg APMQ nội tiếp(tổng 2 góc đối =90)
b) diện tích tam giác AMB=1/2.MP.AB=1/2.MP.BC; diện tích tam giác AMC=1/2.MQ.AC=1/2.MP.BC( AB=BC=CA tam giác đều)
S tam giác ABC=1/2.AH.BC
ta có: S AMB+S AMC=S ABC <=> \(\frac{1}{2}.MP.BC+\frac{1}{2}MQ.BC=\frac{1}{2}AH.BC\Leftrightarrow\frac{1}{2}BC\left(MP+MQ\right)=\frac{1}{2}.BC.AH\)
=> MP+MQ=AH
c) góc AHM=90(AH là đường cao)=> H cũng thuộc đường tròn đường kính AM <=> ngũ giác APMQH nội tiếp
(O): góc HAQ=1/2 góc HOQ(góc nt và góc ở tâm)
tam giác AHC vuông => góc HAC=90-C=90-60=30 độ hay HAQ=30(góc C=60 vì tam giác đều)
=> góc HOQ=2.30=60 .
(O): góc PAQ=1/2 góc POQ(góc nt và góc ở tâm) <=> góc POQ=2.60=120( góc PAQ hay BAC=60- tam giác đều)
góc HOQ=60 => OH là pg của góc POQ.
tam giác POQ có: OP=OQ=R=> tam giác cân => OH đồng thời là đường cao => OH vuông góc PQ

Ta có: MP vuông góc AB (gt)
=) Góc MPA = 90độ (1)
Lại có: MQ vuông góc AC (gt)
=) Góc MQA = 90 độ (2)
Từ (1) và (2) =) góc MPA + góc MQA = 180độ
Mà 2 góc ở vị trí đối nhau
=) Tứ giác APMQ nội tiếp

a: Xét tứ giác AHEC có
góc AHC=góc AEC=90 độ
=>AHEC nội tiếp
b: AHEC nội tiếp
=>góc HAE=góc HCEvà góc HEA=góc HCA
mà góc HCE=góc HCA
nên góc HAE=góc HEA
=>HE=HA

a) xét tứ giác ABOC có
\(\widehat{ABO}=\widehat{ACO}=90^0\)(tiếp tuyến AB,AC)
=> tứ giác ABOC nội tiếp
b) Xét tam giác ABH zà tam giác AOB có
\(\hept{\begin{cases}\widehat{ABO}chung\\\widehat{BHA}=\widehat{OBA}=90^0\left(BC\perp CA\left(tựCM\right)\right)\end{cases}}\)
=> \(\Delta ABH~\Delta AOB\left(g.g\right)\)
\(=>\frac{AB}{AO}=\frac{AH}{AB}=>AH.AB=AB.AB\left(1\right)\)
xét tam giác ABD zà tam giác AEB có
\(\widehat{BAE}chung\)
\(\widehat{ABD}=\widehat{BEA}\)(cùng chắn \(\widebat{BD}\))
=> \(\Delta ABD~\Delta AEB\left(g.g\right)\)
\(=>\frac{AB}{AE}=\frac{AD}{AB}=>AE.AD=AB.AB\left(2\right)\)
từ 1 zà 2 suy ra
AH.AO=AE.AD(dpcm)
=>\(\Delta ADH~\Delta AOE\)
\(=>\widehat{DEO}=\widehat{DHA}\)(2 góc tương ứng
lại có
\(\widehat{DHA}+\widehat{DHO}=180^0=>\widehat{DEO}+\widehat{DHO}=180^0\)
=> tứ giác DEOH nội tiếp
c) Có tam giá AOM zuông tại O , OB là đường cao
\(=>\frac{1}{OA^2}+\frac{1}{OM^2}=\frac{1}{OB^2}=\frac{1}{R^2}\)
\(\frac{1}{OA.OM}=\frac{1}{OA}.\frac{1}{OM}\le\frac{1}{\frac{OA^2+OM^2}{2}}=\frac{1}{\frac{R^2}{2}}=\frac{1}{2R^2}\left(a,b\le\frac{a^2+b^2}{2}\right)\)
=>\(OA.OM\ge2R^2=>MinS_{AMN}=2R^2\)
dấu = xảy ra khi OA=OM
=> tam giác OAM zuông cận tại O
=> góc A = độ
bài 2
ra kết quả là \(6\pi m^2\)
nếu cần giải bảo mình

a: góc AHM+góc AKM=180 độ
=>AHMK nội tiếp
b: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
góc HBM=góc KCM
=>ΔMHB đồng dạng vơi ΔMKC
=>MH/MK=MB/MC
=>MH*MC=MB*MK

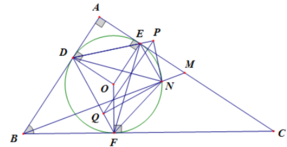
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.

có ai on ko nó chuyện vs mih chứ ai đng xem bóng đá thì cứ xem
A B C M D E 1 1 1 1 2
a) Do ΔABC đều => AB = BC = AC = a; \(\widehat{A}=\widehat{B}=\widehat{C}=60^o\)
Xét ΔBDM vuông tại D có: MD = MB.sin\(\widehat{B}\) = MB.sin60o = MB.\(\dfrac{\sqrt{3}}{2}\)
BD = MB.cos\(\widehat{B}\) = MB.cos60o = \(\dfrac{1}{2}\).MB
ΔCEM vuông tại E có: ME = MC.sin\(\widehat{C}\) = MC.sin60o = MC.\(\dfrac{\sqrt{3}}{2}\)
EC = MC.cos\(\widehat{C}\) = MC.cos60o = \(\dfrac{1}{2}\).MC
=> Chu vi tứ giác ADME là:
AD + AE + MD + ME = (AB - BD) + (AC - CE) + MB.\(\dfrac{\sqrt{3}}{2}\) + MC.\(\dfrac{\sqrt{3}}{2}\)
= AB + AC - (BD + CE) + \(\dfrac{\sqrt{3}}{2}\)(MB + MC)
= AB + AC - \(\dfrac{1}{2}\).(MB + MC) + \(\dfrac{\sqrt{3}}{2}\)(MB + MC)
= AB + AC + \(\dfrac{\left(\sqrt{3}-1\right)}{2}\).BC
= a + a + \(\dfrac{\left(\sqrt{3}-1\right)}{2}\).a = \(\dfrac{3+\sqrt{3}}{2}\).a
Do a không đổi => chu vi tứ giác ADME không đổi
b) Xét ΔBMD vuông tại D => \(\widehat{M_1}=90^o-\widehat{B}=90^o-60^o=30^o\)
ΔCME vuông tại E => \(\widehat{M_2}=90^o-\widehat{C}=90^o-60^o=30^o\) =>
Tứ giác BDEC nội tiếp đường tròn ⇔ \(\widehat{E_2}=\widehat{B}=60^o\)
Mà \(\widehat{B}=\widehat{C}=60^o\) (cmt) => \(\widehat{E_2}=\widehat{C}\). Mà 2 góc ở vị trí đồng vị => DE // BC
=> \(\left\{{}\begin{matrix}\widehat{D_1}=\widehat{M_1}=30^o\\\widehat{E_1}=\widehat{M_2}=30^o\end{matrix}\right.\)(hai góc so le trong)
=> \(\widehat{D_1}=\widehat{E_1}\left(=30^o\right)\)
=> ΔMDE cân tại M => MD = ME
=> \(\dfrac{\sqrt{3}}{2}\).MB = \(\dfrac{\sqrt{3}}{2}\).MC => MB = MC => M là trung điểm của BC
Vậy để tứ giác BDEC nội tiếp thì M là trung điểm của BC