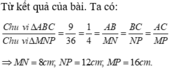Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

\(\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{1}{2}\)
\(\Leftrightarrow S_{ABC}=2\cdot S_{MNP}=2\cdot15=30\left(cm\right)\)

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: \(MN=\dfrac{BC}{2}=6\left(cm\right)\)
Xét ΔABC có
M là trung điểm của AB
P là trung điểm của BC
Do đó: MP là đường trung bình của ΔBAC
Suy ra: \(MP=\dfrac{AC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Xét ΔABC có
N là trung điểm của AC
P là trung điểm của BC
Do đó: NP là đường trung bình của ΔBAC
Suy ra: \(NP=\dfrac{AB}{2}=4\left(cm\right)\)
Chu vi tam giác MNP là:
C=MN+MP+NP=4+5+6=15(cm)

A B C G M N P
a) Xét tg AGB có: M là trung điểm của GA (gt); N là trung điểm của GB (gt)
\(\Rightarrow\)MN là đường trung bình của tg \(\Rightarrow\)MN= 1/2 AB \(\Rightarrow\)MN/AB =1/2
CM tương tự: MP/AC =1/2 ; NP/BC =1/2
Xét tg MNP và tg ABC có: MN/AB =1/2 (cmt); MP/AC =1/2 (cmt); NP/BC =1/2 (cmt)
\(\Rightarrow\)tg MNP \(\infty\)tg ABC (c.c.c) theo tỉ số 1/2
b) tg MNP \(\infty\)tg ABC (c.c.c) theo tỉ số 1/2 \(\Rightarrow\)\(\frac{P\Delta MNP}{P\Delta ABC}=\frac{1}{2}\)mà \(P\Delta MNP=18cm\Rightarrow\)\(P\Delta ABC=\)2.18=36cm
(mk vẽ hình hơi xấu thông cảm nha)

M; N; Q lần lượt là trung điểm của AB; AC; BC (gt)
=> MN; NQ; MQ là đường trung bình của tam giác ABC (đn)
=> MN = 1/2BC ; NQ = 1/2AB; MQ = 1/2AC (đl)
=> MN + NQ + MQ = 1/2BC + 1/2AB + 1/2AC
=> MN + NQ + MQ = 1/2(AB + AC + BC)
chu vi của tam giác ABC = 48 cm (gt) => AB + AC + BC = 48
=> MN + NQ + MQ = 1/2*48 = 24
có NQ : MN : MQ = 9 : 8 : 7
=> NQ/9 = MN/8 = MQ/7
=> (NQ + MN + MQ)/(9 + 8 + 7) = NQ/9 = MN/8 = MQ/7
=> 24/24 = NQ/9 = MN/8 = MQ/7
=> 1 = NQ/9 = MN/8 = MQ/7
=> NQ = 9; MN = 8; MQ = 7
từ đó tính ra các cạnh