1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.a. tứ giác ACOD là hình jb. tam giác BCD là tam giác jc. tính chu vi và diện tích tam giác BCD3. tam giác ABC nhọn nội tiếp...
Đọc tiếp
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với


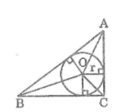

Gọi D, E, F lần lượt là tiếp điểm của (O) với BC, AC, AB
\(\Rightarrow OD\perp BC\) ; \(OE\perp AC\) ; \(OF\perp AB\)
Và \(OD=OE=OF=R\)
Ta có:
\(S_{ABC}=S_{OAB}+S_{OAC}+S_{OBC}\)
\(=\dfrac{1}{2}OF.AB+\dfrac{1}{2}OE.AC+\dfrac{1}{2}OD.BC\)
\(=\dfrac{1}{2}R.AB+\dfrac{1}{2}R.AC+\dfrac{1}{2}R.BC\)
\(=\dfrac{1}{2}R.\left(AB+AC+BC\right)\)
\(\Rightarrow45=\dfrac{1}{2}R.30\)
\(\Rightarrow R=3\left(cm\right)\)