Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, chứng minh tam giác EHB và tam giác DHC đồng dạng theo trường hợp G-G
chứng minh được HE/HD=HB/HC
xét tam giác EHD và tam giác BHC có: 2 cạnh tỉ lệ trên= nhau và góc EHD = góc BHC( đđ)
suy ra 2 tam giác đồng dạng
suy ra 2 góc cần cm bằng nhau
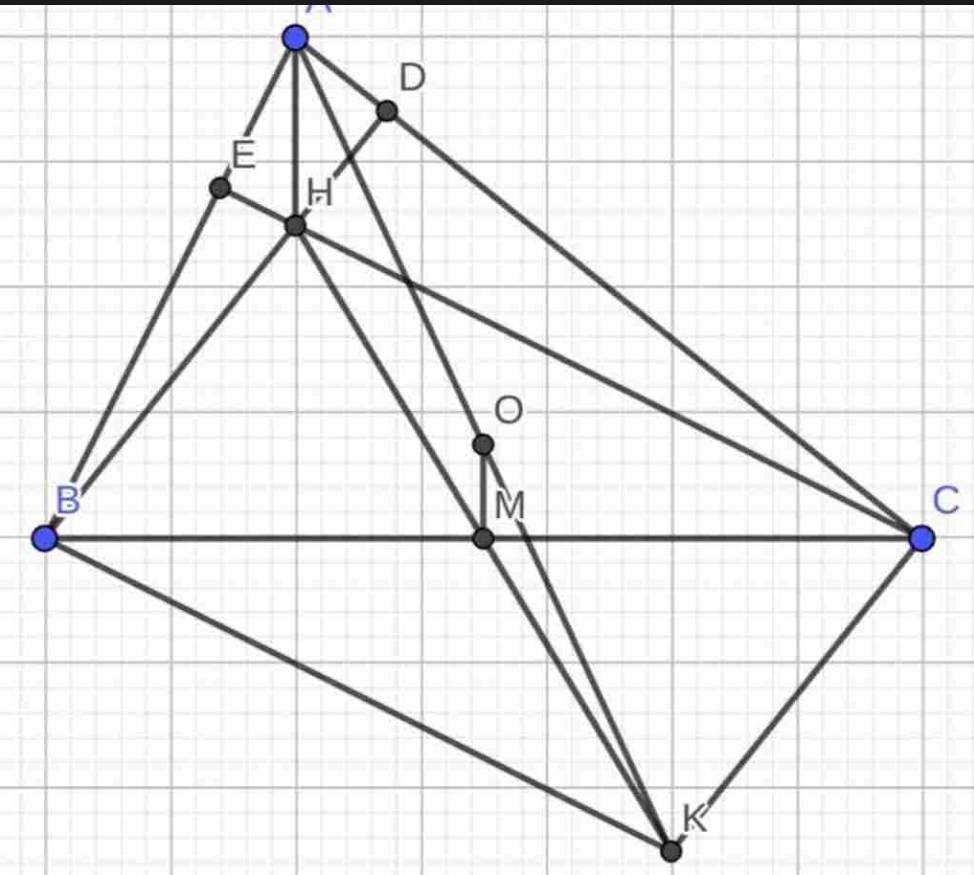
Cho tam giác ABC, các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và vuông góc với AC tại C cắt nhau ở K. Gọi M là trung điểm của BC.
a)Chứng minh tam giác ADB đồng dạng tam giác AEC
Xét tam giác ABD và tam giác ACE có
góc ABD= góc AEC (=90 độ)
góc A: chung
=> tam giác ABD đồng dạng tam giác AEC (g.g)
b) Cm :HE.HC=HD.HB
Xét tam giác HEB và tam giác HDC có
góc HEB= góc HDC (=90 độ)
góc EHB= góc DHC ( đối đỉnh)
=>tam giácHEB đồng dạng tam giác HDC(g.g)
=>HE/HD=HB/HC
<=> HE.HC= HD.HB
c) Cm: H,M,K thẳng hàng
Có BD vuông góc AC
CK vuông góc AC
=> BD song song CK hay BH song song CK
Có CE vuông góc AB
BK vuông góc AB
=> CE song song BK hay CH song song BK
Tứ giác BHCK có BH song song CK
CH song song BK
=> BHCK là hbh ( dhnb)
Mà M là trung điểm của đg chéo BC
=> M cũng là trung điểm của đg chéo HK
=> H,M,K thẳng hàng

a) Có góc A chung và 2 góc vuông => ĐPCM
b) Xét EHB và DHC có:
2 góc vuông và 2 góc đối đỉnh EHB và DHC
=> EHB đồng dạng với DHC
=>BH/CH=EH/DH
=>BH.DH=EH.CH
c)Từ câu a ta suy ra được tỉ số : AB/AC=AD/AE
và có góc A chung .
Từ đó suy ra: ADE đồng dạng với ABC
=> góc ADE= góc ABC
d) Ta có IO là đường trung bình ( tự chứng minh )
=> IO//AH => AHM đồng dạng với IOM
Tỉ số cạnh = AM/IM =2 ( do là đường trung bình )
Tỉ số diện tích của AHM so với IOM là 22=4
Vậy SAHM=4.SIOM

a: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>H,M,K thẳng hàng
b: BHCK là hình thoi khi BH=HC
=>AB=AC

c: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hbh
=>M là trung điểm của HK
=>H,M,K thẳng hàng
d: BACK là hình thoi
=>M là trung điểm của AK và AK vuông góc BC
=>A,H,M thẳng hàng
=>ΔABC cân tại A
=>AB=AC
tham khảo
a.Ta có BK//CH(⊥AB),CK//BH(⊥AC)BK//CH(⊥AB),CK//BH(⊥AC)
→BHCK→BHCK là hình bình hành
b.Vì BHCKBHCK là hình bình hành
→HK∩BC→HK∩BC tại trung điểm mỗi đường
Do MM là trung điểm BCBC
→M→M là trung điểm HKHK
→H,M,K→H,M,K thẳng hàng
c.Ta có O,MO,M là trung điểm AK,HKAK,HK
→OM→OM là đường trung bình ΔAHKΔAHK
→OM//AH→OM//AH
Do BD∩CE=H→HBD∩CE=H→H là trực tâm ΔABC→AH⊥BCΔABC→AH⊥BC
→OM⊥BC