
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(\Leftrightarrow AB=10\cdot\dfrac{\sqrt{3}}{3}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin30^0=\dfrac{AB}{BC}\)
\(\Leftrightarrow BC=\dfrac{10\sqrt{3}}{3}:\dfrac{1}{2}=\dfrac{10\sqrt{3}}{3}\cdot2=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)

a: \(\widehat{B}=90^0-30^0=60^0\)
XétΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}\)
nên AB=5cm
=>\(AC=5\sqrt{3}\left(cm\right)\)
b: \(\widehat{C}=90^0-30^0=60^0\)
Xét ΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}\)
hay \(BC=16\sqrt{3}\left(cm\right)\)
=>\(AC=8\sqrt{3}\left(cm\right)\)

Trả lời:
Tam giác ABC có:
Sin B = AC/BC (hệ thức lượng)
=> AC = Sin B.BC = Sin 450 . 10 = 5√2 (cm)
Sin C = AB/BC
=> AB = Sin 300 . 10 = 5 (cm)
Ta có tam giác ABC có: góc A + góc B + góc C = 1800
=> góc A = 1800 - 450 - 300 = 1050
Tam giác ABC có: Sin B = ACBCACBC (hệ thức lượng) => AC = Sin B.BC = Sin 450 . 10 = 5√252 (cm)
Sin C = ABBCABBC (hệ thức lượng) => AB = Sin 300 . 10 = 5 (cm)
Ta có tam giác ABC có: góc A + góc B + góc C = 1800 (định lý)
=> góc A = 1800 - 450 - 300 = 1050

góc B=90-30=60 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>AB/10=1/2
=>AB=5cm
=>\(AC=5\sqrt{3}\left(cm\right)\)
HB=AB^2/BC=2,5cm
HC=BC-BH=10-2,5=7,5cm

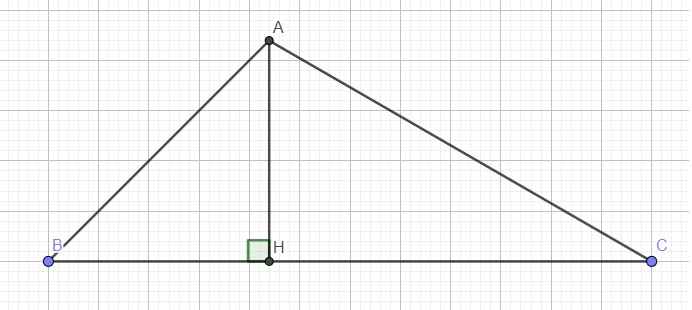
Kẻ đường cao AH
Trong tam giác vuông ABH:
\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)
Trong tam giác vuông ACH:
\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)
\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)
\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)
\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{BC^2}{cotB+cotC}=\dfrac{1}{2}.\dfrac{6^2}{cot45^0+cot30^0}\approx11,4\left(cm^2\right)\)
Tam giác ABC có: Sin B = \(\frac{AC}{BC}\) (hệ thức lượng) => AC = Sin B.BC = Sin 450 . 10 = \(5\sqrt{2}\) (cm)
Sin C = \(\frac{AB}{BC}\) (hệ thức lượng) => AB = Sin 300 . 10 = 5 (cm)
Ta có tam giác ABC có: góc A + góc B + góc C = 1800 (định lý)
=> góc A = 1800 - 450 - 300 = 1050
Chúc bạn học tốt!
vì tam giác ABC khg phải tam giác vuông nên cách làm trên sai