Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 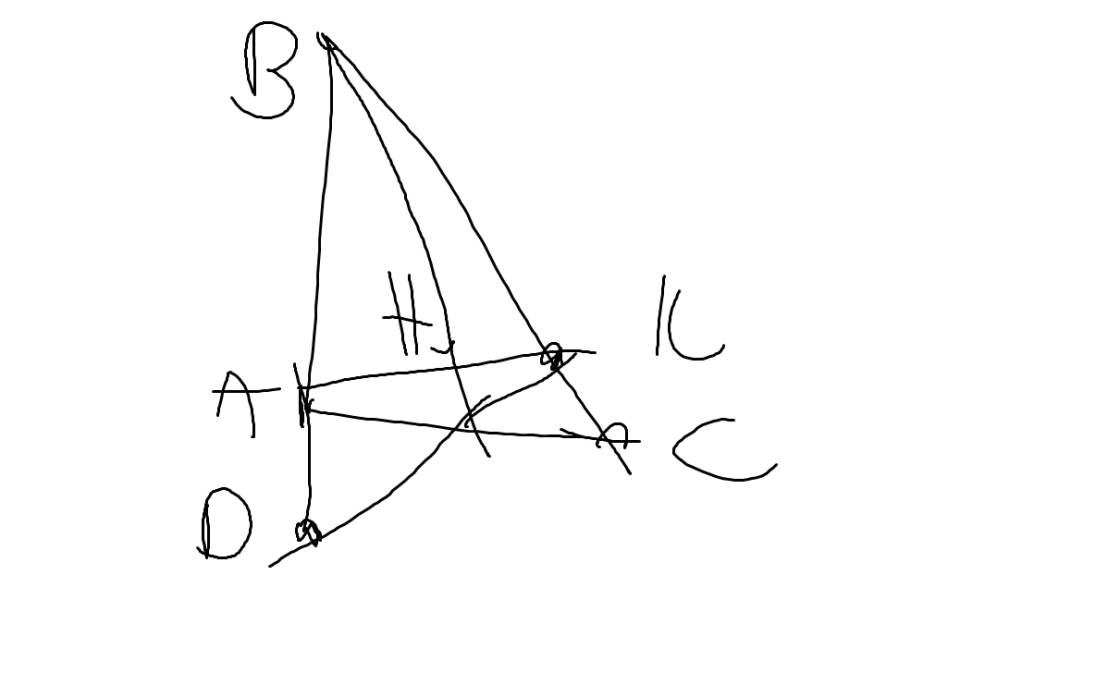
b: Xét ΔBAH và ΔBKH có
BA=BK
AH=KH
BH chung
Do đó: ΔBAH=ΔBKH
c: Sửa đề: Cm BH\(\perp\)AK
Ta có: ΔBAK cân tại B
mà BH là đường trung tuyến
nên BH là đường cao
=>BH\(\perp\)AK
d: Xét ΔBDC có \(\dfrac{BA}{AD}=\dfrac{BK}{KC}\)
nên AK//DC

Tự vẽ hình được nha bạn ^^.
a, Vì M là trung điểm của đoạn thẳng BD
=> MB = MD = BD: 2
Xét tam giác ADM và tam giác ABM:
AM: Cạnh chung
AB = AD
MB = MD ( chứng minh trên )
Do đó: \(\Delta ABM=\Delta ADM\left(c.c.c\right)\)
Phần b sai đề, vì phần c có liên quan đến phần b mà phần b sai đề => phần c cũng sai đề

D A C E K M B 1 2 1 2 3 4 1 2 1 2
Xét 2 tam giác ABM và ADM có
AB = AD
BM = DM => tam giác ABM = tam giác ADM (c.c.c)
Cạnh AM chung
=> A1 = A2
B1 = D1
M1 = M2
Vì M1 kề bù với M2
=> M1 + M2 = 180
=>2 M1 = 180
=> M1 = 90
=< M2 = 90
Vì M1 kề bù vs M4
M2 kề bù vs M3
=> M1 + M4 = M2 + M3 = 180
Mà M1 = M2 = 90
=> M4 = 180 - 90 = 90
M3 = 180 - 90 = 90
=> M3 = M4
Xét 2 tam giác KMD và KMB có :
M3 = M4
BM = DM => tam giác KMD = tam giác KMB (c.g.c)
MK là cạnh chung
=> BK = DK
Xét 2 tam giác ABK và ADK có :
AB = AD
BK = DK => tam giác ABK = ADK (c.c.c)
AK là cạnh chung
b) Đợi tý , tớ suy nghĩ đã
theo tớ , đề câu a phải là :
AM cắt cạnh BC tại K.Chứng minh tam giác ABK=tam giác ADK

a)xet tam giac abd va tam giac aed co
ab=ae
ad la canh chunggoc bad = goc ead
=>tam giác abd = ead
b)gọi i là giao điểm của ad và be
xét tam giác abi và tam giác aei có :
ab=ae
ad là cạnh chung
goc bai = góc eai
=> tam giác abi= tâm giác aei
=>ib=ie =>ad là đường trung trực của be
cho mk 3 đi mk giải tiếp cho, bài nay mk vừa mới kiểm tra
mk giải tiếp nè
theo câu a,b=>góc dbf= góc dec (kề bù do góc abd= aed)
xét tam giác bfd và ecd có
góc dbf= góc dec
bd=ed
bdf=edc
=> tam giác dbf= tam giác ecd
k cho mk đi.mk hứa mk tl hết cho mà
A B C D K E
a, xét tam giác ADC và tam giác AKB có : ^BAC chung
AB = AC (gt)
AD = AK (gt)
=> tam giác ADC = tam giác AKB (c-g-c)
=> DC = BK (đn)
b, AB = AC (gt)
AD = AK (gt)
AD + BD = AB
AK + KC = AC
=> KC = BD (1)
tam giác ADC = tam giác AKB (Câu a) => ^ADC = ^AKB (đn)
^ADC + ^CDB = 180 (kb)
^AKB + ^BKC = 180 (kb)
=> ^CDB = ^BKC
xét tam giác EDB và tam giác EKC có : ^DBE = ^KCE do ...
và (1)
=> tam giác EDB = tam giác EKC (g-c-g)