Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b/ ta có: Góc DAE = 360 - (90 . 2) - góc A = 180 - 110 = 70 độ
từ tam giác ABM = tam giác KCM => AB = CK
Xét tam giác CAK & tam giác AED có:
KCA = DAE (bằng 70 độ)
AD = CK (bằng AB)
AC = AE (gt)
=> tam giác CAK = tam giác AED (cgc)
b, vì tam giác ABM=tam giác KCM(câu a) =>AB=CK(2 cạnh tương ứng)
mà AB=AD(gt) =>KC=AD
Có DAE+DAB+EAC+BAC=3600=>DAE=3600-(DAB+EAC+BAC)
mả DAB=900(AD vuông góc vs AB-GT)
EAC=900(AE vuông góc vs AC-GT)
BAC=1100 (GT)
=>DAE=3600-(900+900+1100)=700
Có DAE=700(CMT)
ACK=700(câu a)
=>DAE=ACK(=700)
Xét tam giác CAK & tam giác AED có:
CK=AD(cmt)
CA=AE(gt)
DAE=ACK(cmt)
=>tam giác CAK=tam giác AED(c.g.c)
phần c mik k bit lm giúp nhé

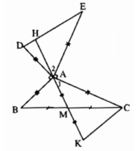
Có: ∠DAE + ∠DAB + ∠BAC + ∠CAE = 360o
Mà ∠DAB = ∠CAE = 90o; ∠BAC = 110o
⇒ ∠DAE = 70o
⇒ ∠DAE = ∠ACK
+) Xét ΔCAK và ΔAED có:
AC = AE (gt)
∠ACK = ∠DAE (chứng minh trên)
CK = AD (cùng = AB)
⇒ ΔCAK = ΔAED (c.g.c)

A B C D E G F H M N
ta có góc DAC = góc EAB = 90 độ (gt)
suy ra \(\widehat{DAB}+\widehat{BAC}=\widehat{EAC}+\widehat{BAC}\) (vì tia AB nằm giữa 2 tia AD và AC , tia AC nằm giữa 2 tia AE và AB )
hay \(\widehat{DAC}=\widehat{EAB}\)
\(\Delta DAC\)và\(\Delta BAE\)có \(\hept{\begin{cases}AD=AB\left(gt\right)\\\widehat{DAC}=\widehat{EAB}\left(cmt\right)\\AE=AC\left(gt\right)\end{cases}}\)
do đó \(\Delta DAC=\Delta BAE\left(c.g.c\right)\)
suy ra \(DC=BE\)(2 góc tương ứng)
và \(\widehat{EBA}=\widehat{CDA}\)( 2 góc tương ứng )
gọi giao điểm của AB và CD là G , giao điểm của DC và BE là F
\(\Delta ADG\)và \(\Delta GBF\)có \(\hept{\begin{cases}\widehat{D}=\widehat{B}\left(cmt\right)\\\widehat{DGA}=\widehat{BGF}\\\Rightarrow\widehat{BFG}=\widehat{DAG}=90^o\end{cases}}\)(đối đỉnh)
hay \(BE⊥DC\)
b) ta có góc DAH là góc ngoài của tam giác AMD
suy ra \(\widehat{DAH}=\widehat{AMD}+\widehat{ADM}\) hay \(\widehat{DAB}+\widehat{BAH}=\widehat{AMD}+\widehat{ADM}\)(vì tia AB nằm giữa 2 tia AD và AH )
mà \(\widehat{DAB}=\widehat{AMD}=90^o\)\(\Rightarrow\widehat{BAH}=\widehat{ADM}\)
\(\Delta ABH\)và\(\Delta DAM\)có \(\hept{\begin{cases}DA=BA\left(gt\right)\\\widehat{BAH}=\widehat{ADM}\left(cmt\right)\end{cases}}\)
do đó \(\Delta ABH=\Delta DAM\)(cạnh huyền - góc nhọn )
suy ra AH =DM ( 2 cạnh tương ứng )
theo đề và từ hình vẽ ta có MN trùng AH
ta có góc EAH là góc ngoài của tam giác ANE
\(\Rightarrow\widehat{EAH}=\widehat{ANE}+\widehat{AEN} hay \widehat{EAC}+\widehat{HAC}=\widehat{ANE}+\widehat{AEN}\)
mà \(\widehat{EAC}=\widehat{ANE}=90^o\)\(\Rightarrow\widehat{HAC}=\widehat{AEN}\)
\(\Delta ACH\)và\(\Delta EAN\)có
cạnh huyền AC = cạnh huyền AE
\(\widehat{HAC}=\widehat{AEN}\left(cmt\right)\)
do đó \(\Delta ACH=\Delta EAN\)(cạnh huyền góc nhọn )
suy ra AH = NE ( 2 cạnh tương ứng )
mà AH =DM
suy ra DM = NE
ta có \(DM⊥NH;EN⊥NH\Rightarrow\)DM//EN
gọi giao điểm của DE và NH là T
xét tam giác vuông MTD và tam giác vuông NTE
góc MDT = góc NET ( so le trong )
DM = NE (cmt)
do đó \(\Delta MDT=\Delta NET\)(cạnh huyền góc nhọn )
suy ra DN = NE ( 2 cạnh tương ứng ) (1)
\(\Delta MDT\)và \(\Delta NET\)có \(\hept{\begin{cases}\widehat{MDT}=\widehat{NET}\\\widehat{DMT}=\widehat{ENT}=90^o\\\Rightarrow\widehat{DTM}=\widehat{ETN}\end{cases}}\)
ta có \(\widehat{NTE}+\widehat{MTE}=180^o\)( kề bù )
mà \(\widehat{NTE}=\widehat{DTM}\left(cmt\right)\)\(\Rightarrow\widehat{MTE}+\widehat{DTM}=180^o\)hay D;N;E thẳng hàng (2)
từ (1) và (2) suy ra N là trung điểm D;E
hay MN và AH đi qua trung điểm DE
câu c gửi bạn sau mk đi học r
chúc bạn học tốt