Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B1:
a) xét 2 tam giác vuông ABH và ACK có:
góc BAC chung
AB = AC (gt)
góc ABH = góc ACK (cùng phụ vs góc ABC)
=> tam giác ABH = tam giác ACK (g.c.g)
b) tam giác ABH = tam giác ACK (câu a)
=> AK = AH mà AB = AC = AK + BK = AH + CH => BK = CH (1)
do AK = AH => tam giác AKH cân tại A => góc AKH = góc AHK = (1800 - góc BAC) : 2 (*)
ta có: góc ABC = góc ACB = (1800 - góc BAC ) : 2 (**)
từ (*) và (**) => góc ABC = góc AKH (đồng vị ) => BC // KH (2)
từ (1) và (2) => tứ giác BCHK là hình thang đều
t i c k nhé!! 3543645767658587687689698797808657568568

Hih e tự vẽ nha:
a) Vì DM//BE nên tứ giác BDME là hình thang.
Lại có :\(\widehat{B}=\widehat{C}=60\)( tam giác ABC đều)
và \(\widehat{BEM}=\widehat{C}=60\)(Vì DE//AC và ACB=90 độ)
=>\(\widehat{BEM}=\widehat{B}=60\)
=>Tứ giác BDME là htc.
T/tự cho các hình còn lại.
b)Xét tam giác BDM và EMD:
BD=ME( BDME là htc)
góc BDM=góc EMD(Vì DM//BE và góc BEM=góc B=60 độ)
DM là cah chug
=> tg BDM=tg EMD (cgc)
=>BM=DE
C/m t/tự đối vói các tg AFD=AMF; tg CEM=tg FME
=> AM=DF;CM=EF
=>BM+AM+CM=DE+DF+EF= Chu vi của tam giác DEF
c) Ở câu a/ ta đã có góc B= góc E=60 nên suy ra đc các góc còn lại của htc BDME bằng 120 độ
T/tự cho 2 htc còn lại suy ra đc cả 3 góc đều =120 độ nên chúng = nhau
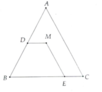
M A B C D E F
a, Chứng minh các tứ giác BDME,CFME,ADMF là các hình hang cân.
Ta có : MD//BC\(\Rightarrow\)BDME là hình thang cân .(1)
ME//AC\(\Rightarrow\widehat{MEB}=\widehat{ACB}\)(hai góc đồng vị )
mà \(\widehat{ACB}=\widehat{ABC}=60^o\)(do tam giác ABC đều)
\(\Rightarrow\widehat{MEB}=\widehat{ABC}=60^o\)(2)
Từ (1) và (2) => tứ giác BDME là hình thang cân.
Chứng minh tương tự ta cũng có : tứ giác CFME và ADMF là các hình thang cân.
b,Chứng minh chu vi của tam giác DEF bằng tổng các khoảng cách từ M đến các đỉnh của tam giác ABC . \(\left(P_{DME}=MB+MA+MC\right)\)
Ta có : \(P_{DEF}=DE+DF+EF\)
Lại có tứ giác BDME là hình thang cân (cmt) => DE = MB.
tứ giác CFME là hình thang cân (cmt)=> MC=EF
tứ giác DMF là hình thang cân (cmt)=> MA =DF.
\(\Rightarrow P_{DEF}=MA+MB+MC\)
=> đpcm.
c,Chứng minh \(\widehat{DME}=\widehat{DMF}=\widehat{EMF}\)
Trong hình thang cân BDME có : \(\widehat{DBE}=60^o\)
mà \(\widehat{DME}+\widehat{DBE}=180^o\Rightarrow\widehat{DME}=180^o-\widehat{DBE}=180^o-60^o=120^o\)
Chứng minh tương tự ta có : \(\widehat{DMF}=120^o;\widehat{EMF}=120^o\)
=>\(\widehat{DME}=\widehat{DMF}=\widehat{EMF}=120^o\)(đpcm)
Mình giải chi tiết rùi đấy nhé nếu có j hk hiểu cứ nhắn tin cho mk mk sẽ giải thích cho nhé.
Nên nhớ hình vẽ chỉ mang tính chất minh họa . Mình vẽ hình cho mấy bạn nhìn vô cho dể hiểu thôi chứ chưa chuẩn lắm đâu mấy bạn tự vẽ hình cho đẹp nhé ai thấy hay thì k cho mk nhé . CẢM ƠN NHIỀU .