Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

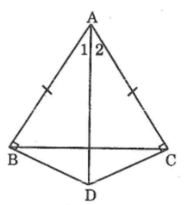
Xét hai tam giác vuông ABD và ACD, ta có:
∠(ABD) =∠(ACD) =90o
Cạnh huyền AD chung
AB = AC (giả thiết)
⇒ ΔABD= ΔACD (cạnh huyền, cạnh góc vuông)
Suy ra: ∠(A1 ) =∠(A2) (hai góc tương ứng)
Suy ra AD là tia phân giác góc A

Xét tam giác ADB và tam giac ADC có :
AD chung
Góc ABD=góc ACD=90 0
AB=AC(2 tam giác cân tại a)
=>tam giác ADB=tam giác ADC (ch-cgv)
=>góc BAD = góc CAD (góc tương ứng)
Vậy AD là tia phân giác góc A
Duyệt nha
Xét tam giác ADB và tam giác ADC có:
AD chung
góc ABD=góc ACD=90 độ
AB=AC(tam giác ABC cân tại A)
=> tam giác ADB=tam giác ADC(ch-cgv)
=> góc BAD=góc CAD(góc tương ứng)
Vậy AD là tia phân giác góc A
tik cho mk nha các bn

a) Gọi G, F lần lượt là chân đường vuông góc từ O kẻ xuống AB và AC
Ta có: O nằm trên đường trung trực của AB(gt)
mà OG⊥AB(gt)
nên G là trung điểm của AB
Ta có: O nằm trên đường trung trực của AC(gt)
mà OF⊥AC(gt)
nên F là trung điểm của AC
Ta có: \(AG=\dfrac{AB}{2}\)(G là trung điểm của AB)
\(AF=\dfrac{AC}{2}\)(F là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AG=AF
Xét ΔAGO vuông tại G và ΔAFO vuông tại F có
AO chung
AG=AF(cmt)
Do đó: ΔAGO=ΔAFO(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{GAO}=\widehat{FAO}\)(hai góc tương ứng)
hay \(\widehat{BAO}=\widehat{CAO}\)
mà tia AO nằm giữa hai tia AB,AC
nên AO là tia phân giác của \(\widehat{BAC}\)(đpcm)
c) Xét ΔAOB và ΔAOC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAO}=\widehat{CAO}\)(cmt)
AO chung
Do đó: ΔAOB=ΔAOC(c-g-c)
Suy ra: OB=OC(hai cạnh tương ứng)
Ta có: \(\widehat{ABC}+\widehat{KBC}=\widehat{ABK}\)(tia BC nằm giữa hai tia BA,BK)
nên \(\widehat{ABC}+\widehat{KBC}=90^0\)(1)
Ta có: \(\widehat{ACB}+\widehat{KCB}=\widehat{ACK}\)(tia CB nằm giữa hai tia CA,CK)
nên \(\widehat{ACB}+\widehat{KCB}=90^0\)(2)
Từ (1) và (2) suy ra \(\widehat{ABC}+\widehat{KBC}=\widehat{ACB}+\widehat{KCB}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{KBC}=\widehat{KCB}\)
Xét ΔKBC có \(\widehat{KBC}=\widehat{KCB}\)(cmt)
nên ΔKBC cân tại K(Định lí đảo của tam giác cân)
Suy ra: KB=KC(hai cạnh bên)
Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBEC=ΔCDB(cạnh huyền-góc nhọn)
Suy ra: \(\widehat{BCE}=\widehat{CBD}\)(hai góc tương ứng)
hay \(\widehat{HBC}=\widehat{HCB}\)
Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)(cmt)
nên ΔHBC cân tại H(Định lí đảo của tam giác cân)
Suy ra: HB=HC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: HB=HC(cmt)
nên H nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Ta có: KB=KC(cmt)
nên K nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(6)
Từ (3), (4), (5) và (6) suy ra A,O,H,K thẳng hàng(đpcm)

a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó; ΔABD=ΔACD
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD

a) Gọi G, F lần lượt là chân đường vuông góc từ O kẻ xuống AB và AC
Ta có: O nằm trên đường trung trực của AB(gt)
mà OG⊥AB(gt)
nên G là trung điểm của AB
Ta có: O nằm trên đường trung trực của AC(gt)
mà OF⊥AC(gt)
nên F là trung điểm của AC
Ta có: AG=AB2AG=AB2(G là trung điểm của AB)
AF=AC2AF=AC2(F là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AG=AF
Xét ΔAGO vuông tại G và ΔAFO vuông tại F có
AO chung
AG=AF(cmt)
Do đó: ΔAGO=ΔAFO(cạnh huyền-cạnh góc vuông)
Suy ra: ˆGAO=ˆFAOGAO^=FAO^(hai góc tương ứng)
hay ˆBAO=ˆCAOBAO^=CAO^
mà tia AO nằm giữa hai tia AB,AC
nên AO là tia phân giác của ˆBACBAC^(đpcm)
c) Xét ΔAOB và ΔAOC có
AB=AC(ΔABC cân tại A)
ˆBAO=ˆCAOBAO^=CAO^(cmt)
AO chung
Do đó: ΔAOB=ΔAOC(c-g-c)
Suy ra: OB=OC(hai cạnh tương ứng)
Ta có: ˆABC+ˆKBC=ˆABKABC^+KBC^=ABK^(tia BC nằm giữa hai tia BA,BK)
nên ˆABC+ˆKBC=900ABC^+KBC^=900(1)
Ta có: ˆACB+ˆKCB=ˆACKACB^+KCB^=ACK^(tia CB nằm giữa hai tia CA,CK)
nên ˆACB+ˆKCB=900ACB^+KCB^=900(2)
Từ (1) và (2) suy ra ˆABC+ˆKBC=ˆACB+ˆKCBABC^+KBC^=ACB^+KCB^
mà ˆABC=ˆACBABC^=ACB^(hai góc ở đáy của ΔABC cân tại A)
nên ˆKBC=ˆKCBKBC^=KCB^
Xét ΔKBC có ˆKBC=ˆKCBKBC^=KCB^(cmt)
nên ΔKBC cân tại K(Định lí đảo của tam giác cân)
Suy ra: KB=KC(hai cạnh bên)
Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
ˆEBC=ˆDCBEBC^=DCB^(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBEC=ΔCDB(cạnh huyền-góc nhọn)
Suy ra: ˆBCE=ˆCBDBCE^=CBD^(hai góc tương ứng)
hay ˆHBC=ˆHCBHBC^=HCB^
Xét ΔHBC có ˆHBC=ˆHCBHBC^=HCB^(cmt)
nên ΔHBC cân tại H(Định lí đảo của tam giác cân)
Suy ra: HB=HC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: HB=HC(cmt)
nên H nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Ta có: KB=KC(cmt)
nên K nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(6)
Từ (3), (4), (5) và (6) suy ra A,O,H,K thẳng hàng(đpcm)

A B C _ _ D
Ta có:
ABD=ABC+CBD
ACD=ACB+BCD
Mà ABD=ACD (=90o)
ABC=ACB (\(\Delta\)ABC cân)
\(\Rightarrow\)CBD=BCD
\(\Rightarrow\Delta\)BDC cân
Xét \(\Delta\)ABD và \(\Delta\) ACD có:
AB=AC (\(\Delta\)ABC cân)
AD: chung
BD=CD (\(\Delta\)BDC cân)
\(\Rightarrow\Delta\)ABD=\(\Delta\)ACD (c.c.c)
\(\Rightarrow\)BAD=CAD (2 góc tương ứng)
\(\Rightarrow\)AD là p/g BAC (đpcm)
Ta có tam giác ABC la tam giác cân tại A
=> AB = AC ( tính chất tam giác cân )
Xét tam giác ABD vuông tại B và tam giác ACD vuông tại C có :
AB = Ac ( cmt )
Ad là cah chung
=> tam giác ABD = tam giác ACD ( ch -cgv )
=> Góc A1 = góc A2 ( hai góc tương ứng )
=> AD là tia phân giác góc A
Xét tam giác ADB và tam giác ADC có:
AD chung
Góc ABD=góc ACD=90o
AB=AC(tam giác ABC cân tại A)
=> tam giác ADB=tam giác ADC(ch-cgv)
=> Góc BAD=góc CAD(góc tương ứng)
Vậy AD là tia phân giác góc A
tik nha=)))))))))))))
123cm2
duyet di