Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình sẽ làm từ câu C nha vì câu C có liên quan đến câu cuối
c/ Xét tam giác ABF và tam giác AEC ta có :
Góc BAF = góc CAE ( AF là phân giác)
góc ABF = góc AEC ( 2 góc nt chắn cung AC)
=>tam giác ABF đồng dạng tam giác AEC (g-g)
=>\(\frac{AB}{AE}=\frac{AF}{AC}\)=>AB.AC=AE.AF
d/ Xét tam giác ABF và tam giác CFE ta có:
góc ABF = góc FEC ( 2 góc nt chắn cung AC )
góc BAF = góc FCE (2 góc nt chắn cung EB )
=> tam giác ABF đồng dạng tam giác CEF (g-g)
=>\(\frac{FB}{FE}=\frac{FA}{FC}\)=>FB.FC=FA.FE
Ta có AF.AE=AB.AC (cmt)
AF.FE=BF.CF (cmt)
=> AF.AE-AF.FE = AB.AC - BF.CF
=> AF(AE-FE) = AB.AC - BF.CF
=> \(AF^2=AB.AC-BF.CF\)

a) Xét (O) có AE là tia phân giác của góc BAC
=> ^BAE=^CAE
=> sđBE=sđCE
=> BE=CE (liên hệ giữa cung và dây cung)
=> tam giác BEC cân tại E (đpcm)
b) Tứ giác ABEC nội tiếp (O)
=> ^BAC+^BEC=180 độ (2 góc đối nhau)
<=> ^BEC=180 độ - ^BAC
Tam giác ABC có ^BAC+^ABC+^BCA=180 độ
=> =180 độ - ^BAC=^ABC+^BCA
Suy ra Góc BEC = góc ABC + góc ACB (đpcm)
c) AE là tia phân giác của góc BAC
=> ^BAE=^CAE
Hay ^BAF=^CAE
Tứ giác ABEC nội tiếp (O)
=> ^ABC=^AEC (2 góc nt chắn cung AC)
Hay ^ABF=^AEC
Xét tam giác ABF và tam giác AEC có:
^ABF=^AEC
^BAF=^CAE
=> tam giác ABF ~ tam giác AEC (g-g)
=> AB/AF=AE/AC
<=> AB.AC=AE.AF (đpcm)

a) Xét (O) có :
AB là tiếp tuyến tại B
AC là tiếp tuyến tại C
AB cắt AC tại A
\(\Rightarrow\widehat{ABO}=\widehat{ACO}=90^o\)và OA là p/g \(\widehat{BOC}\)
Xét tg ABOC có \(\widehat{ABO}+\widehat{ACO}=180^o\)Mà 2 góc này đối nhau
\(\Rightarrow\)ABOC là tg nt
b) Xét (O) có
\(\widehat{ABE}\)là góc tạo bởi tiếp tuyến AB và dây BE
\(\widehat{BDE}\)là góc nt chắn cung BE
\(\Rightarrow\widehat{ABE}=\widehat{BDE}=\frac{1}{2}sđ\widebat{BE}\)
Xét \(\Delta ABEvà\Delta ADB:\)
\(\widehat{BAD}\)chung
\(\widehat{ABE}=\widehat{BDE}\)
\(\Rightarrow\Delta ABE\infty\Delta ADB\left(gg\right)\)
\(\Rightarrow\frac{AB}{AD}=\frac{AE}{AB}\Rightarrow AB^2=AD.AE\)
c) Vì OA là p/g \(\widehat{BOC}\Rightarrow\widehat{BOA}=\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Do ABOC là tg nt\(\Rightarrow\widehat{BOA}=\widehat{BCA}\)(cùng chắn cung AB)
Suy ra \(\widehat{AOC}=\widehat{ACB}\)

O A B C D E
a, vì \(AD\) là tia phân giác của góc \(\widehat{BAC}\) \(\Rightarrow\widehat{BAD}=\widehat{EAC}\)
mà \(\widehat{ABD}=\widehat{ABC}=\widehat{AEC}\)
\(\Rightarrow\Delta ABD~\Delta AEC\) (g-g)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AC}\Leftrightarrow AB.AC=AE.AD\)
b, Ta có :
\(\widehat{EBD}=\widehat{EBC}=\widehat{EAC}=\widehat{BAE}\)
\(\Rightarrow\Delta EBD~\Delta EAB\)(g-g)
\(\Rightarrow\frac{EB}{EA}=\frac{ED}{EB}\Leftrightarrow ED.EA=EB^2\)
a)xét ΔABE và ΔADC có :
BÅE = DÅC (gt)
AEB=ACB=ACD(cùng chắn cung AB)
=>ΔABE≈ΔADC(g.g)
⇒\(\dfrac{AE}{AC}=\dfrac{AB}{AD}\)(hai cạnh t.ứ)
⇒AE.AD=AC.AB
b)Xét ΔBED và ΔAEB có :
góc E chung
góc EBD=gócEAC=gócEAB
⇒ΔBED ≈ ΔAEB(g.g)
⇒\(\dfrac{ED}{EB}=\dfrac{EB}{EA}\)(hai cạnh t.ứ)
⇒ED.EA=EB2

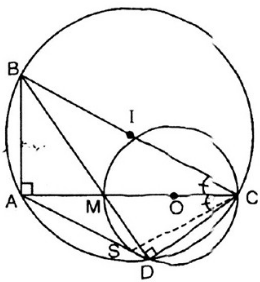
a, ta có ^BAC=900(góc nội tiếp chắn nửa đường tròn đường kính BC)
^MDC=900(góc nội tiếp chắn nửa đường tròn đường kính MC)
=>^BAC=^MDC(=900)
=>tứ giác ABCD nội tiếp (hai đỉnh A và D kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau)
b. vì tứ giác ABCD nội tiếp (câu a) nên ^ABD=^ACD (hai góc nội tiếp cùng chắn cung AD)
c, ta có bốn điểm D,S,C,M cùng thuộc đường tròn đường kính MC
=>tứ giác DSCM nội tiếp
=>^ADM=^SCM (cùng bù với ^MDS)
Mà ADCB nội tiếp nên ^ADM=^MCB( hai góc nội tiếp cùng chắn cung AB)
Do đó ^SCM=^MCB
=>CA là tia phân giác ^SCB